第二类边界条件下固液相变问题的改进型准稳态近似解

杨小虎; 李少丹; 陈凯

doi:10.21656/1000-0887.420141

第二类边界条件下固液相变问题的改进型准稳态近似解

doi: 10.21656/1000-0887.420141

武汉第二船舶设计研究所热能动力技术重点实验室，武汉 430205

基金项目: 国家自然科学基金（52006158）；湖北省自然科学基金（2020CFB462）

详细信息

作者简介:
杨小虎（1991—），男，高级工程师，博士（通讯作者. E-mail：yangxhcsic@163.com）

中图分类号: TK02
计量
- 文章访问数: 501
- HTML全文浏览量: 288
- PDF下载量: 68
- 被引次数: 0
出版历程
- 收稿日期: 2021-05-20
- 修回日期: 2021-09-20
- 网络出版日期: 2022-10-10
- 刊出日期: 2022-11-30

Improved Quasi-Steady-State Approximation Analysis of Stefan Problems Under 2nd-Kind Boundary Conditions

Science and Technology on Thermal Energy and Power Laboratory, Wuhan Second Ship Design and Research Institute, Wuhan 430205, P.R.China

摘要

摘要:
基于准稳态近似方法，从热平衡角度出发，给出了直角坐标系和圆柱坐标系中恒定热流边界条件下传导型固液相变传热问题的无量纲近似解。对于直角坐标系情形，得到的改进型准稳态近似解精度高，且解的形式为显式表达式，相比于已有的隐式近似解更便于直接使用。对于圆柱坐标系的情形，所得到的近似解是目前文献公开报道的唯一的近似解。此改进型准稳态近似解弥补了传统准稳态近似方法不考虑显热的不足，提高了准稳态近似法的精度，丰富了固液相变传热问题的求解方法，物理意义明确，可用于实际应用问题的初步分析和计算。
- 储能 /
- 相变材料 /
- Stefan问题 /
- 第二类边界条件 /
- 准稳态近似 /
- 无量纲关系
Abstract:
Improved quasi-steady-state approximation solutions were obtained for Stefan problems under the 2nd-kind boundary conditions, both in Cartesian and cylindrical coordinates, based on the traditional quasi-steady state approximation and the 1st law of thermodynamics. For the Cartesian coordinate condition, the solution has high accuracy, and is convenient for practical use for its explicit form. For the cylindrical coordinate solution, the presented approximation solution is the only solution reported in the related literatures. The proposed improved solutions take sensible heat into consideration and greatly promote the accuracy of traditional methods, and enrich the analysis methods for the Stefan problems, with definite physical meaning of a useful reference for quick preliminary calculation of practical problems.
- energy storage /
- phase change material /
- Stefan problem /
- 2nd-kind boundary condition /
- quasi-steady state approximation /
- dimensionless correlation

HTML全文

图 1 传导型固液相变物理模型：（a）平板单相熔化问题；（b）圆柱体外单相熔化问题

注　为了解释图中的颜色，读者可以参考本文的电子网页版本，后同。

Figure 1. Schematics of single phase Stefan problems: (a) the semi-finite slab; (b) the cylinder

下载: 全尺寸图片幻灯片

图 2 f(S_te)和g(S_te)拟合曲线

Figure 2. Fitting curves of f(S_te) and g(S_te)

下载: 全尺寸图片幻灯片

图 3 Nu·ϕ随S_te的变化

Figure 3. Variation of Nu·ϕ with S_te

下载: 全尺寸图片幻灯片

图 4 线性化温度分布与精确值的对比

Figure 4. Comparison of approximation solutions and exact solutions

下载: 全尺寸图片幻灯片

图 5 恒壁温平板单相熔化问题数值解与精确解对比

Figure 5. Validation of the numerical method

下载: 全尺寸图片幻灯片

图 6 几种近似解与数值解的对比

Figure 6. Comparison of numerical results and approximation results

下载: 全尺寸图片幻灯片

图 7 改进型准稳态近似解与数值解的对比

Figure 7. Comparison of the improved approximation solutions and numerical results

下载: 全尺寸图片幻灯片

图 8 改进型准稳态近似解

Figure 8. Improved quasi-steady-state approximation solutions

下载: 全尺寸图片幻灯片

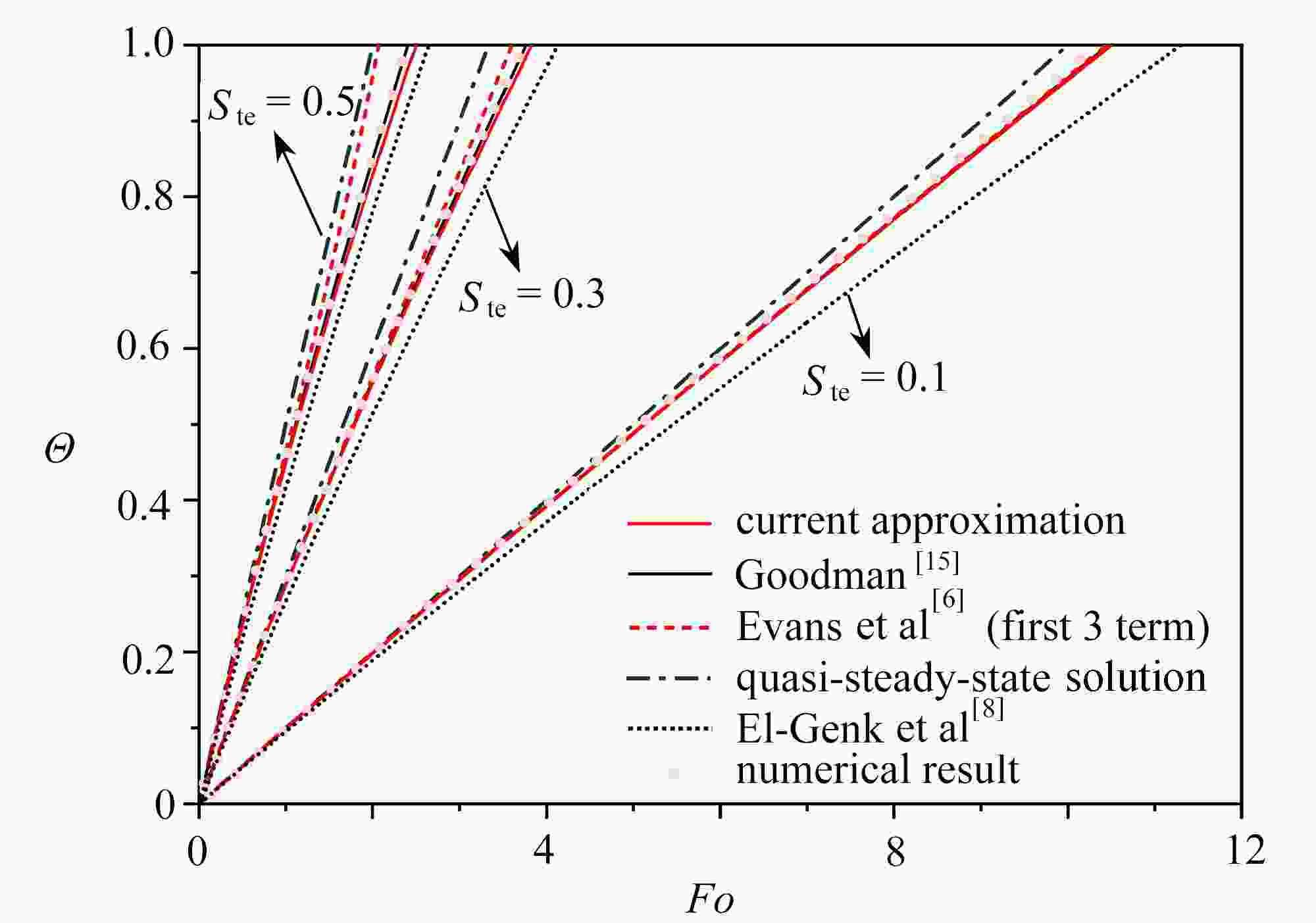
表 1 几种近似解误差对比（以S=1时的Fo作为对比指标）

Table 1. Comparison of different approximate solutions (Fo as the index for S=1)

S_te	numerical result (as reference)	El-Genk et al^[8]	Goodman^[15]	Evans et al^[6]	quasi-steady-state solution	present approximation
0.1	10.372	9.0%	1.0%	0.8%	−3.6%	1.2%
0.3	3.760	9.9%	0.2%	−4.2%	−11.4%	1.9%
0.5	2.407	9.9%	0.2%	−13.8%	−16.9%	3.8%

下载: 导出CSV

参考文献(18)

[1]	ZHAO B C, LI T X, GAO J C, et al. Latent heat thermal storage using salt hydrates for distributed building heating: a multi-level scale-up research[J]. Renewable and Sustainable Energy Reviews, 2020, 121(7): 109712.
[2]	李长玉, 方彦奎, 刘福旭, 等. 热防护服-空气-皮肤热传导模型及其解析解[J]. 应用数学和力学, 2021, 42(2): 162-169 LI Changyu, FANG Yankui, LIU Fuxu, et al. A thermal protective clothing-air-skin heat conduction model and its analytical solution[J]. Applied Mathematics and Mechanics, 2021, 42(2): 162-169.(in Chinese)
[3]	FLEISCHER A S. Thermal Energy Storage Using Phase Change Materials: Fundamentals and Applications[M]. Berlin: Springer, 2015.
[4]	CRANK J. Free and Moving Boundary Problems[M]. Oxford: Clarendon Press, 1984.
[5]	TAO L. On free boundary problems with arbitrary initial and flux conditions[J]. Zeitschrift für Angewandte Mathematik und Physik (ZAMP), 1979, 30(3): 416-426.
[6]	EVANS G, ISAACSON I, MACDONALD J. Stefan-like problems[J]. Quarterly of Applied Mathematics, 1950, 8(3): 312-319. doi: 10.1090/qam/37451
[7]	SCHIAVONE P, CONSTANDA C, MIODUCHOWSKI A. Integral Methods in Science and Engineering[M]. Berlin: Springer Science & Business Media, 2012.
[8]	EL-GENK M S, CRONENBERG A W. Solidification in a semi-infinite region with boundary conditions of the second kind: an exact solution[J]. Letters in Heat and Mass Transfer, 1979, 6(4): 321-327. doi: 10.1016/0094-4548(79)90019-5
[9]	QU P, ZHANG C, LIAO X, et al. A new computation method for solidification process in a finite, initially overheated slab[J]. Journal of Thermal Science, 1992, 1(4): 272-277. doi: 10.1007/BF02653207
[10]	BELI G E. Solidification of a liquid about a cylindrical pipe[J]. International Journal of Heat and Mass Transfer, 1979, 22(12): 1681-1686. doi: 10.1016/0017-9310(79)90084-X
[11]	YANG X H, LIU J. A novel method for determining the melting point, fusion latent heat, specific heat capacity and thermal conductivity of phase change materials[J]. International Journal of Heat and Mass Transfer, 2018, 127(Part B): 457-468.
[12]	CRANK J. Diffusion with rapid irreversible immobilization[J]. Transactions of the Faraday Society, 1957, 53: 1083-1091. doi: 10.1039/tf9575301083
[13]	LIN S, JIANG Z. An improved quasi-steady analysis for solving freezing problems in a plate, a cylinder and a sphere[J]. Journal of Heat Transfer, 2003, 125(6): 1123-1128. doi: 10.1115/1.1622719
[14]	SOLOMON A D. The applicability and extendability of Megerlin’s method for solving parabolic free boundary problems[J]. Moving Boundary Problems, 1977, 1: 187-202.
[15]	GOODMAN T R. The heat-balance integral and its application to problems involving a change of phase[J]. Journal of Fluids Engineering, 1958, 80(2): 335-342. doi: 10.1115/1.4012364
[16]	CARSLAW H S, JAEGER J C. Conduction of Heat in Solids[M]. Oxford: Oxford Clarendon Press, 1959.
[17]	RUKH S, PASHA R A, NASIR M A. Heat transfer enhancement of round pin heat sinks using n-eicosane as PCM: an experimental study[J]. Heat and Mass Transfer, 2019, 55(2): 309-325. doi: 10.1007/s00231-018-2411-6
[18]	ZENG Y, DONG J, KHODADADI J M. Thermal coupling-decoupling mechanism of heat transfer across van der Waals interfaces in n-eicosane[J]. International Journal of Heat and Mass Transfer, 2021, 164(10): 120603.