The Interface Model and the Interphase Model for Predicting the Effective Elastic Properties of Nano-Fiber Composites
-
摘要:
基于广义自洽法，同时采用Gurtin-Murdoch界面模型和界面相模型研究了纳米纤维复合材料的有效弹性性能，获得了两种模型下有效体积模量的封闭解析解和计算有效面内剪切模量数值解的全部公式。基于界面模型的解答，讨论了有效体积模量和有效面内剪切模量的界面效应。证明了界面模型的解答可由界面相模型的解答退化得到，其中有效体积模量可以实现解析退化，有效面内剪切模量则可以数值退化。以含纳米孔洞的金属铝为例，比较了两种模型计算结果的差异。结果表明，当纳米孔洞半径较小时，两个模型的结果存在很大差异，而当半径较大时两个模型的结果差别不大。
Abstract:The effective bulk modulus and the effective in-plane shear modulus of nano-fiber composites were investigated with the interface model and the interphase model based on the generalized self-consistent method, and the closed-form analytical solutions of the effective bulk modulus and all equations for numerically predicting effective in-plane shear modulus based on the 2 models, were presented. With the interface model, interface effects of the effective bulk modulus and the effective in-plane shear modulus were discussed through numerical examples. Furthermore, the solutions of the interface model were proved to be degenerated ones of those of the interphase model, where the effective bulk modulus can be obtained through analytical degeneration and the numerical results of the effective in-plane shear modulus through numerical degeneration. An example of aluminium containing nano voids shows that, the effective bulk modulus and the effective in-plane shear modulus predicted with the interface model have large deviations from those with the interphase model for small void radii, however, small deviations for larger void radii.
-
Key words:
- nano-fiber composite /
- effective elastic property /
- interface model /
- interphase model
-
图 1 预测纳米纤维复合材料有效性质的两种模型：(a) 界面模型； (b) 界面相模型
Figure 1. Two models for predicting the effective elastic properties of nano-fiber composites: (a) the interface model; (b) the interphase model
图 2 无量纲有效体积模量和有效面内剪切模量随纤维半径的变化
Figure 2. Variations of the dimensionless effective bulk modulus and the in-plane shear modulus with the fiber radius
图 3 无量纲有效体积模量和有效面内剪切模量随纤维刚度的变化
Figure 3. Variations of the dimensionless effective bulk modulus and the in-plane shear modulus with the fiber rigidness
图 4 界面模型和界面相模型的结果对比
Figure 4. Results comparisons between the interface model and the interphase model
表 1 体积模量和剪切模量的退化
Table 1. Degradation of the bulk modulus and the shear modulus
$ {E^{{S_{\text{f}}}}} $/(N/m) interphase model t/nm interface model 10−1 10−2 10−3 10−4 10−5 10−6 10 $ {B_{{\text{em}}}}/{B_{\text{m}}} $
$ {\mu _{{\text{em}}}}/{\mu _{\text{m}}} $0.886 87 0.906 10 0.906 77 0.906 82 0.906 83 0.906 83 0.906 83 0.849 55 0.854 38 0.854 38 0.854 38 0.854 38 0.854 38 0.854 61 −10 $ {B_{{\text{em}}}}/{B_{\text{m}}} $
$ {\mu _{{\text{em}}}}/{\mu _{\text{m}}} $0.900 76 0.892 14 0.892 58 0.892 64 0.892 65 0.892 65 0.892 65 0.834 82 0.831 02 0.831 13 0.831 15 0.831 15 0.831 15 0.831 37 
下载: 导出CSV
A-{111} B-{100} t1 t2 t1 t2 bulk modulus B2/GPa 80.90 79.17 74.37 75.21 shear modulus $ {\mu _2} $/GPa 26.75 26.61 21.19 23.46
下载: 导出CSV
C1 界面模型和界面相模型中的对应符号
C1. Conespording symbols in the interface model and the interphase model
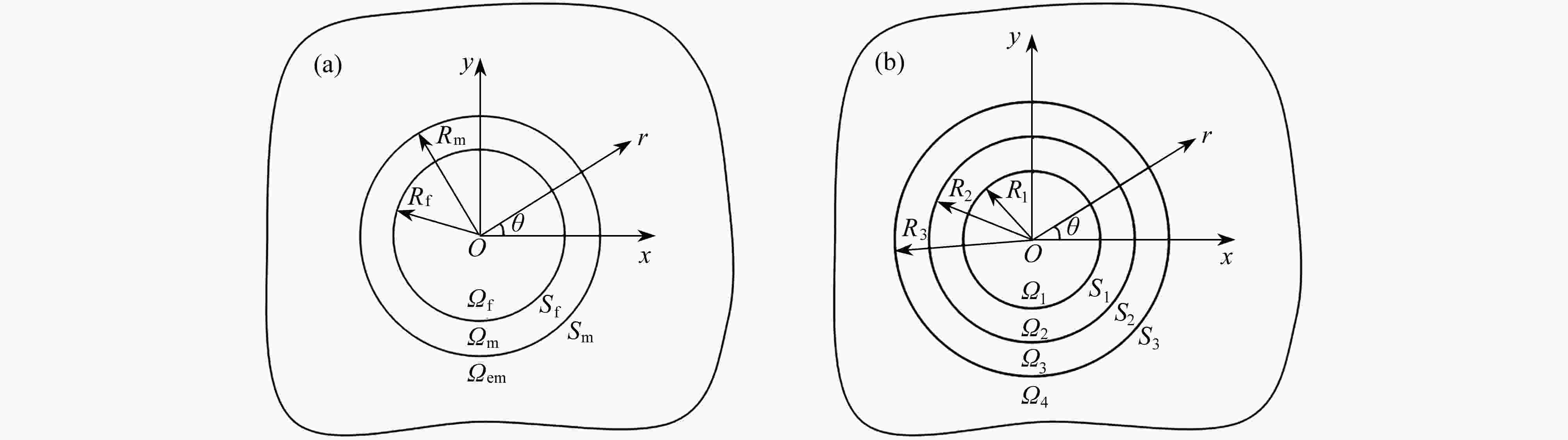
interphase model interface model $ R{}_1 $,$R{}_3$ $ {R_{\text{f}}} $,$ {R_{\text{m}}} $ $ {c_1} $,$ {c_3} $ $ {c_{\text{f}}} $,$ {c_{\text{m}}} $ ${\varGamma _1}$,${\varGamma _3}$ ${\varGamma _{\text{f} } }$,${\varGamma _{\text{m} } }$ ${\varOmega _1}$,${\varOmega _3}$,${\varOmega _4}$ ${\varOmega _{\text{f} } }$,${\varOmega _{\text{m} } }$,${\varOmega _{ {\text{em} } } }$
下载: 导出CSV
-
[1] 刘旭, 姚林泉. 热环境中旋转功能梯度纳米环板的振动分析[J]. 应用数学和力学, 2020, 41(11): 1224-1236LIU Xu, YAO Linquan. Vibration analysis of rotating functionally gradient nano annular plates in thermal environment[J]. Applied Mathematics and Mechanics, 2020, 41(11): 1224-1236.(in Chinese) [2] SHUKLA P, SAXENA P. Polymer nanocomposites in sensor applications: a review on present trends and future scope[J]. Chinese Journal of Polymer Science, 2021, 39(6): 665-691. doi: 10.1007/s10118-021-2553-8 [3] CAMMARATA R C. Surface and interface stress effects on interfacial and nanostructured materials[J]. Materials Science and Engineering: A, 1997, 237(2): 180-184. doi: 10.1016/S0921-5093(97)00128-7 [4] 周强, 张志纯, 龙志林, 等. 考虑表面效应的压电纳米梁的振动研究[J]. 应用数学和力学, 2020, 41(8): 853-865ZHOU Qiang, ZHANG Zhichun, LONG Zhilin, et al. Vibration of piezoelectric nanobeams with surface effects[J]. Applied Mathematics and Mechanics, 2020, 41(8): 853-865.(in Chinese) [5] GURTIN M E, MURDOCH A I. A continuum theory of elastic material surfaces[J]. Archive for Rational Mechanics and Analysis, 1975, 57(4): 291-323. doi: 10.1007/BF00261375 [6] GURTIN M E, MURDOCH A I. Surface stress in solids[J]. International Journal of Solids and Structures, 1978, 14(6): 431-440. doi: 10.1016/0020-7683(78)90008-2 [7] ODEGARD G M, CLANCY T C, GATES T S. Modeling of the mechanical properties of nanoparticle/polymer composites[J]. Polymer, 2005, 46(2): 553-562. doi: 10.1016/j.polymer.2004.11.022 [8] PALIWAL B, CHERKAOUI M. Estimation of anisotropic elastic properties of nanocomposites using atomistic-continuum interphase model[J]. International Journal of Solids and Structures, 2012, 49(18): 2424-2438. doi: 10.1016/j.ijsolstr.2012.05.004 [9] LUO J, WANG X. On the anti-plane shear of an elliptic nano inhomogeneity[J]. European Journal of Mechanics A: Solids, 2009, 28(5): 926-934. doi: 10.1016/j.euromechsol.2009.04.001 [10] TIAN L, RAJAPAKSE R K N D. Analytical solution for size-dependent elastic field of a nanoscale circular inhomogeneity[J]. Journal of Applied Mechanics, 2007, 74(3): 568-574. doi: 10.1115/1.2424242 [11] TIAN L, RAJAPAKSE R K N D. Elastic field of an isotropic matrix with a nanoscale elliptical inhomogeneity[J]. International Journal of Solids and Structures, 2007, 44(24): 7988-8005. doi: 10.1016/j.ijsolstr.2007.05.019 [12] DONG C Y, PAN E. Boundary element analysis of nano-inhomogeneities of arbitrary shapes with surface and interface effects[J]. Engineering Analysis With Boundary Elements, 2011, 35(8): 996-1002. doi: 10.1016/j.enganabound.2011.03.004 [13] MOGILEVSKAYA S G, CROUCH S L, STOLARSKI H K. Multiple interacting circular nano-inhomogeneities with surface/interface effects[J]. Journal of the Mechanics and Physics of Solids, 2008, 56(6): 2298-2327. doi: 10.1016/j.jmps.2008.01.001 [14] DUAN H L, WANG J, HUANG Z P. Size-dependent effective elastic constants of solids containing nano-inhomogeneities with interface stress[J]. Journal of the Mechanics and Physics of Solids, 2005, 53(7): 1574-1596. doi: 10.1016/j.jmps.2005.02.009 [15] CHEN T Y, DVORAK G J, YU C C. Solids containing spherical nano-inclusions with interface stresses: effective properties an thermal-mechanical connections[J]. International Journal of Solids and Structures, 2007, 44(3/4): 941-955. [16] 肖俊华, 徐耀玲, 王美芬, 等. 考虑界面应力时纳米涂层纤维增强复合材料的有效力学性能[J]. 固体力学学报, 2013, 34(4): 374-379 doi: 10.3969/j.issn.0254-7805.2013.04.007XIAO Junhua, XU Yaoling, WANG Meifen, et al. Effective mechanical property of nano coated fiber reinforced composites due to interface stress[J]. Chinese Journal of Solid Mechanics, 2013, 34(4): 374-379.(in Chinese) doi: 10.3969/j.issn.0254-7805.2013.04.007 [17] LI Y, WAAS A M, ARRUDA A E. A closed-form, hierarchical, multi-interphase model for composites-derivation, verification and application to nanocomposites[J]. Journal of the Mechanics and Physics of Solids, 2011, 59(1): 43-63. doi: 10.1016/j.jmps.2010.09.015 [18] PALIWAL B, CHERKAOUI M. Atomistic-continuum interphase model for effective properties of composite materials containing nano-inhomogeneities[J]. Philosophical Magazine, 2011, 91(30): 3905-3930. doi: 10.1080/14786435.2011.597361 [19] WANG Z, OELKERS R J, LEE K C, et al. Annular coated inclusion model and applications for polymer nanocomposites, part Ⅰ: spherical inclusions[J]. Mechanics of Materials, 2016, 101: 170-184. doi: 10.1016/j.mechmat.2016.07.004 [20] WANG Z, OELKERS R J, LEE K C, et al. Annular coated inclusion model and applications for polymer nanocomposites, part Ⅱ: cylindrical inclusions[J]. Mechanics of Materials, 2016, 101: 50-60. doi: 10.1016/j.mechmat.2016.07.005 [21] BENVENISTE Y, MILOH T. Imperfect soft and stiff interfaces in two-dimensional elasticity[J]. Mechanics of Materials, 2001, 33(6): 309-323. doi: 10.1016/S0167-6636(01)00055-2 [22] WANG J, DUAN H L, ZHANG Z. An anti-interpenetration model and connections between interphase and interface models in particle-reinforced composites[J]. International Journal of Mechanical Sciences, 2005, 47(4/5): 701-718. [23] MUSKHELISHIVILI N I. Some Basic Problem of the Mathematical Theory of Elasticity[M]. Leyden: Noordhoff International Publishing, 1977. [24] PARVANOVA S L, VASILEV G P, DINEVA P S, et al. Dynamic analysis of nano-heterogeneities in a finite-size solid by boundary and finite element methods[J]. International Journal of Solids and Structures, 2016, 80(1): 1-18. [25] WANG W F, ZENG X W, DING J P. Finite element modeling of two-dimensional nanoscale structures with surface effects[J]. World Academy of Science, Engineering and Technology, 2010, 48: 865-870. [26] TIAN L, RAJAPAKSE R K N D. Finite element modelling of nanoscale inhomogeneities in an elastic matrix[J]. Computational Materials Science, 2004, 41(1): 44-53. -
计量
- 文章访问数: 606
- HTML全文浏览量: 287
- PDF下载量: 44
- 被引次数: 0
渝公网安备50010802005915号