Study on Droplets Impacting on Orifice Plates With Different Wettabilities Based on the Lattice Boltzmann Method
-
摘要:
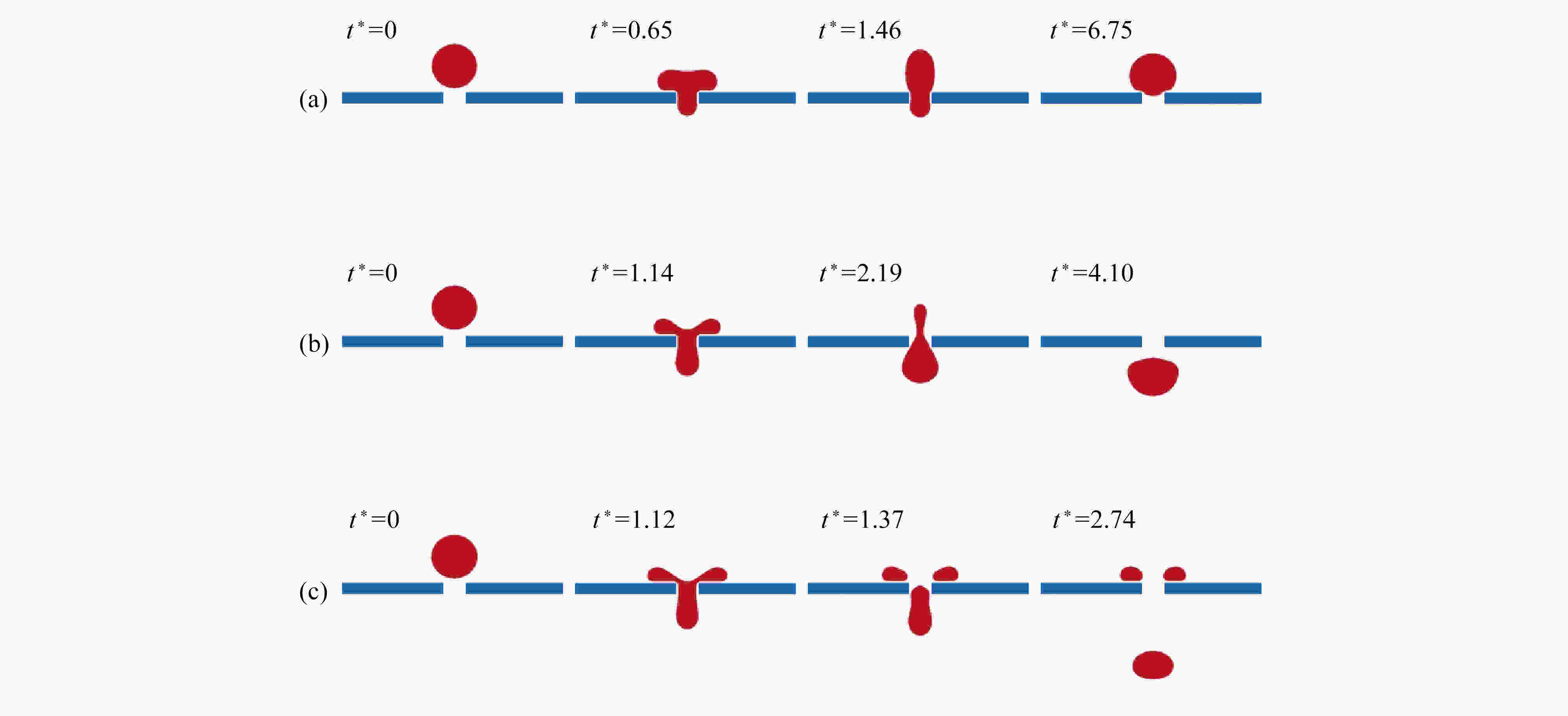
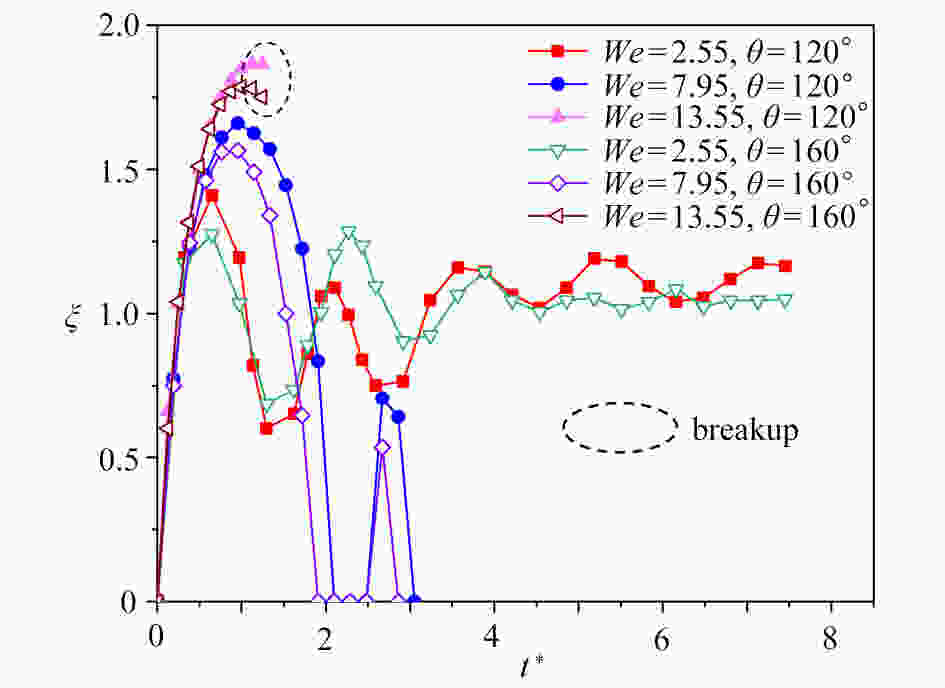
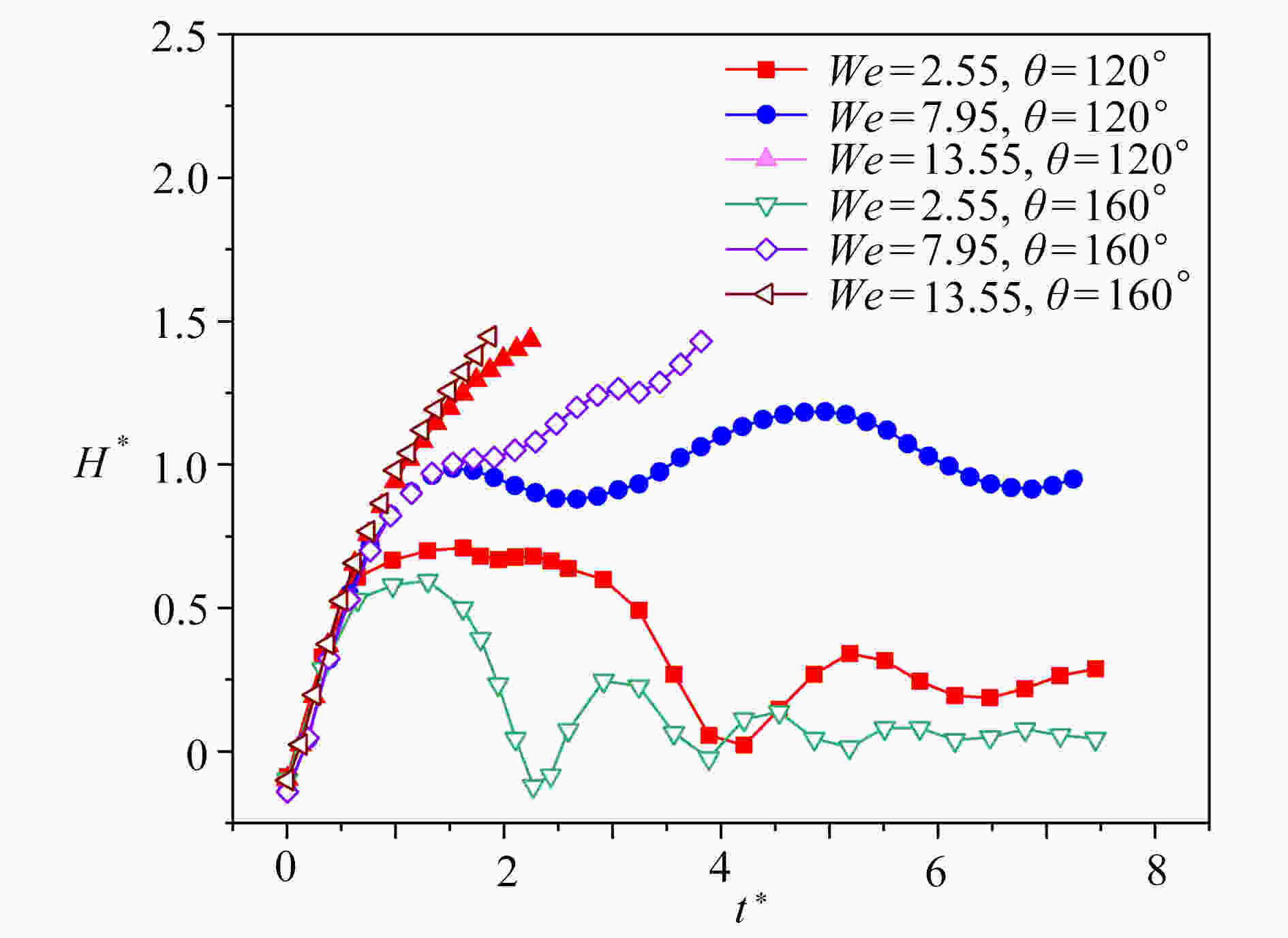
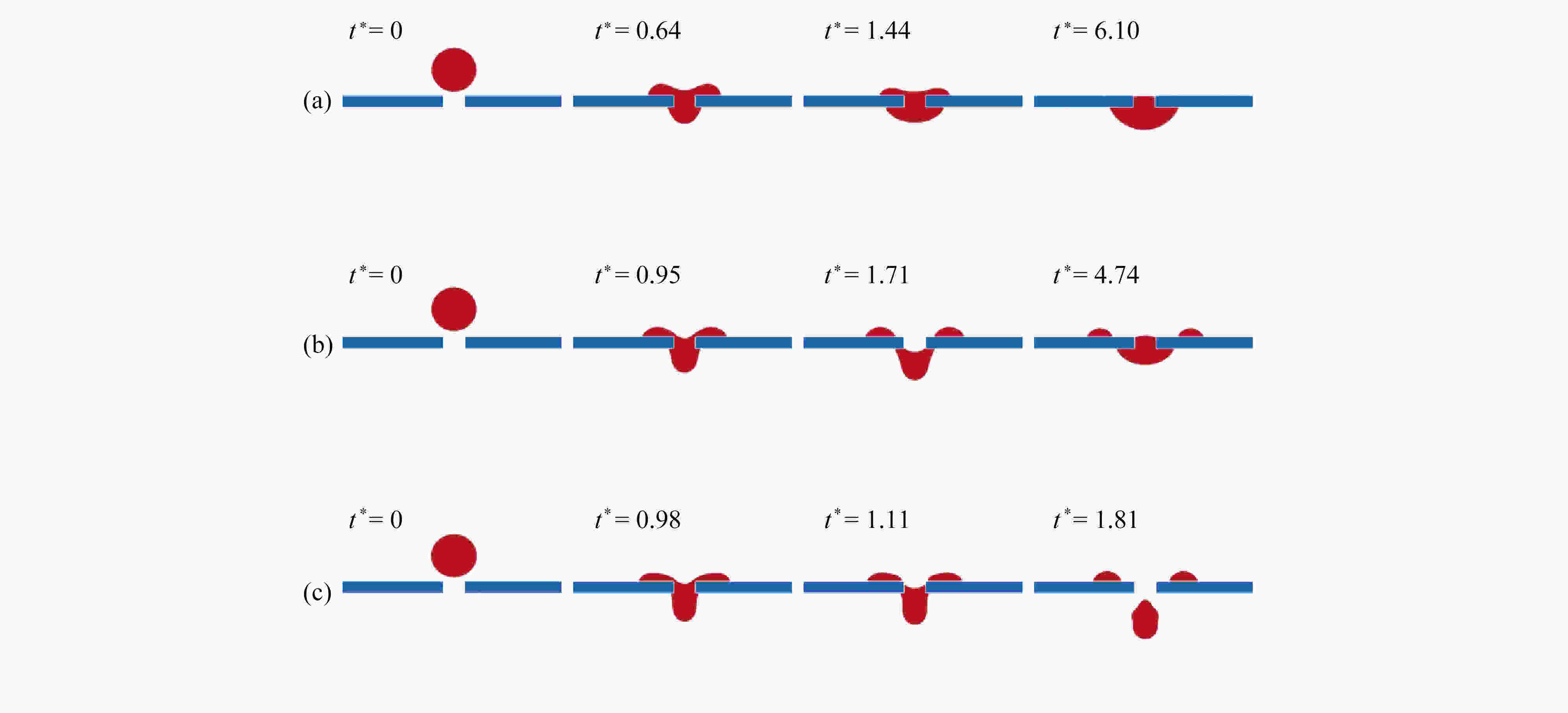
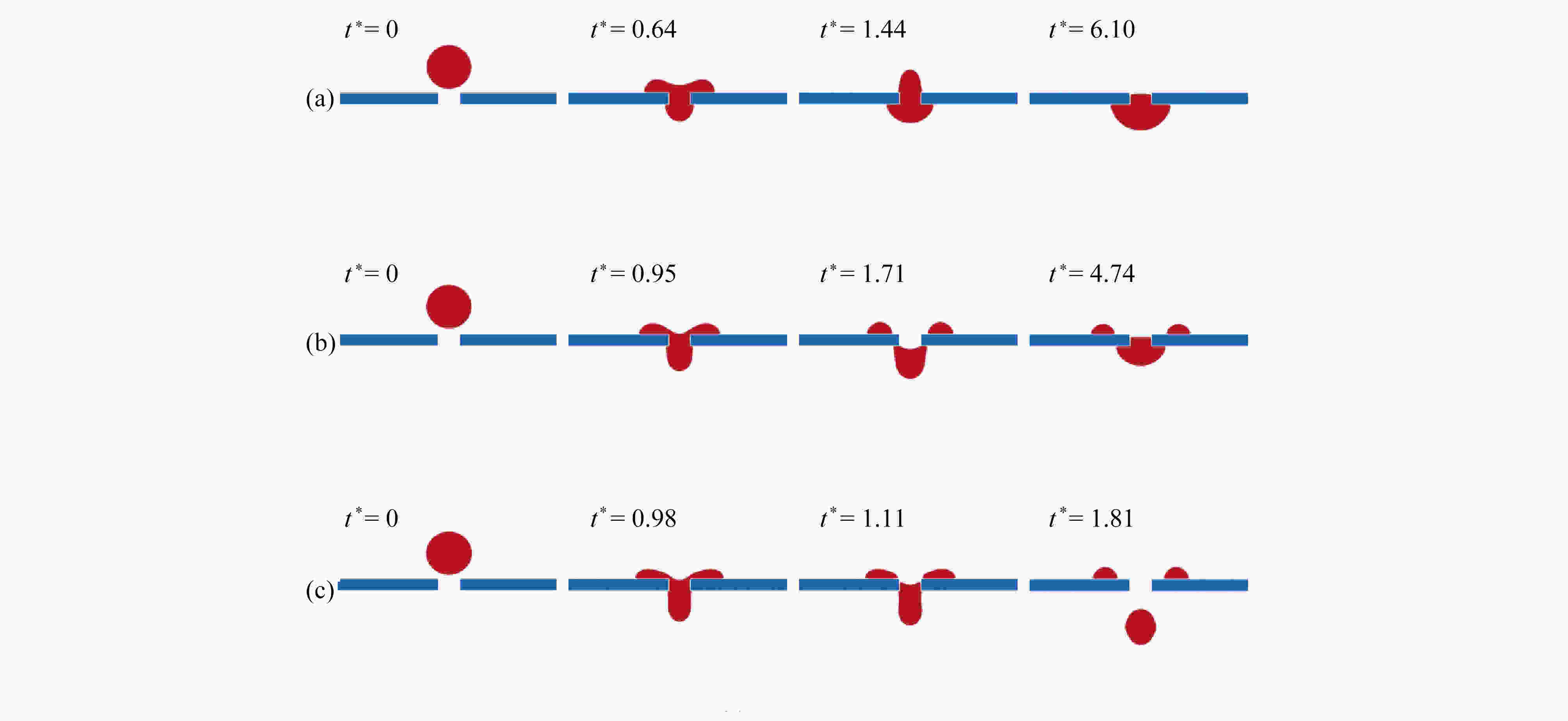
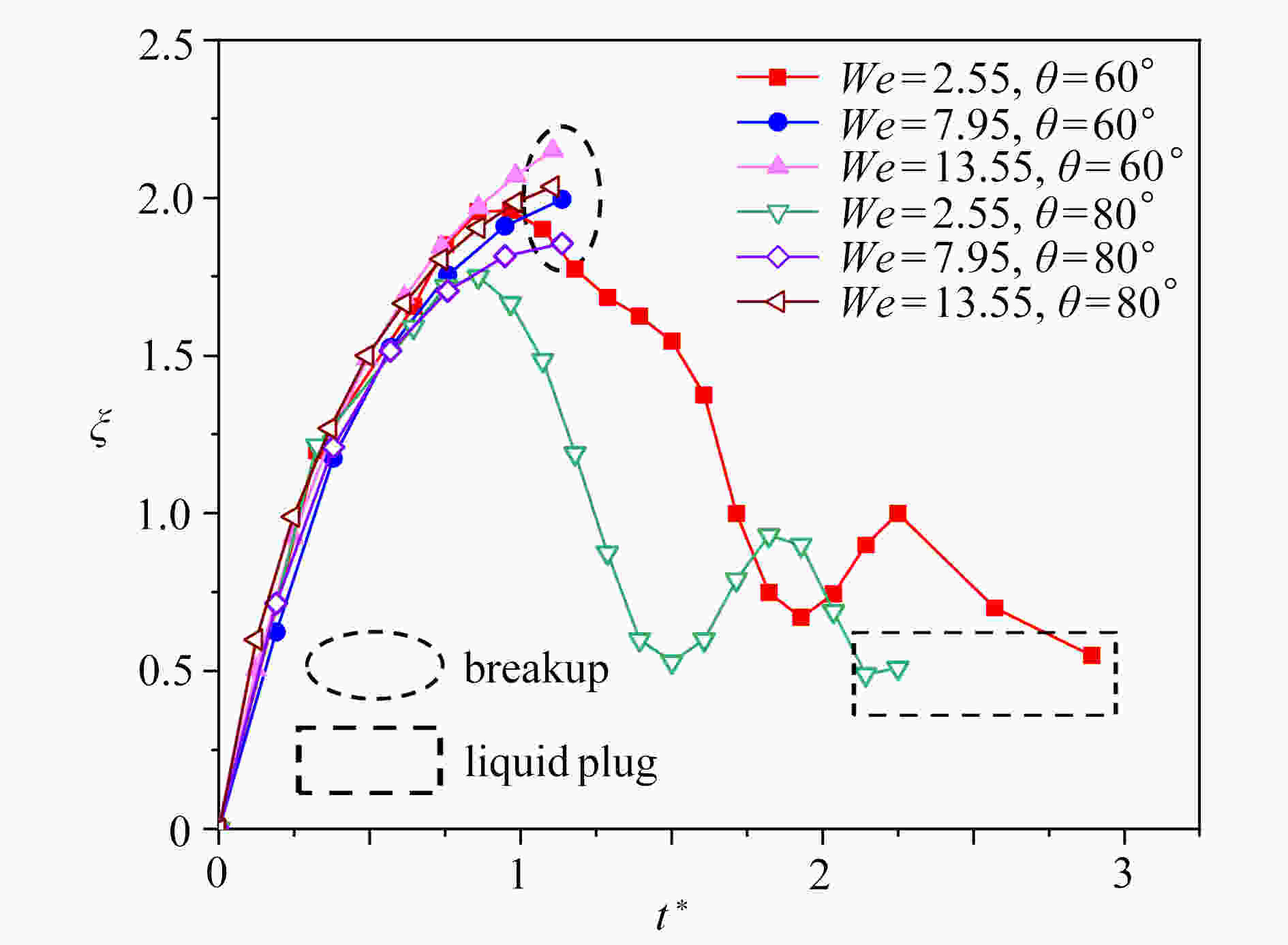
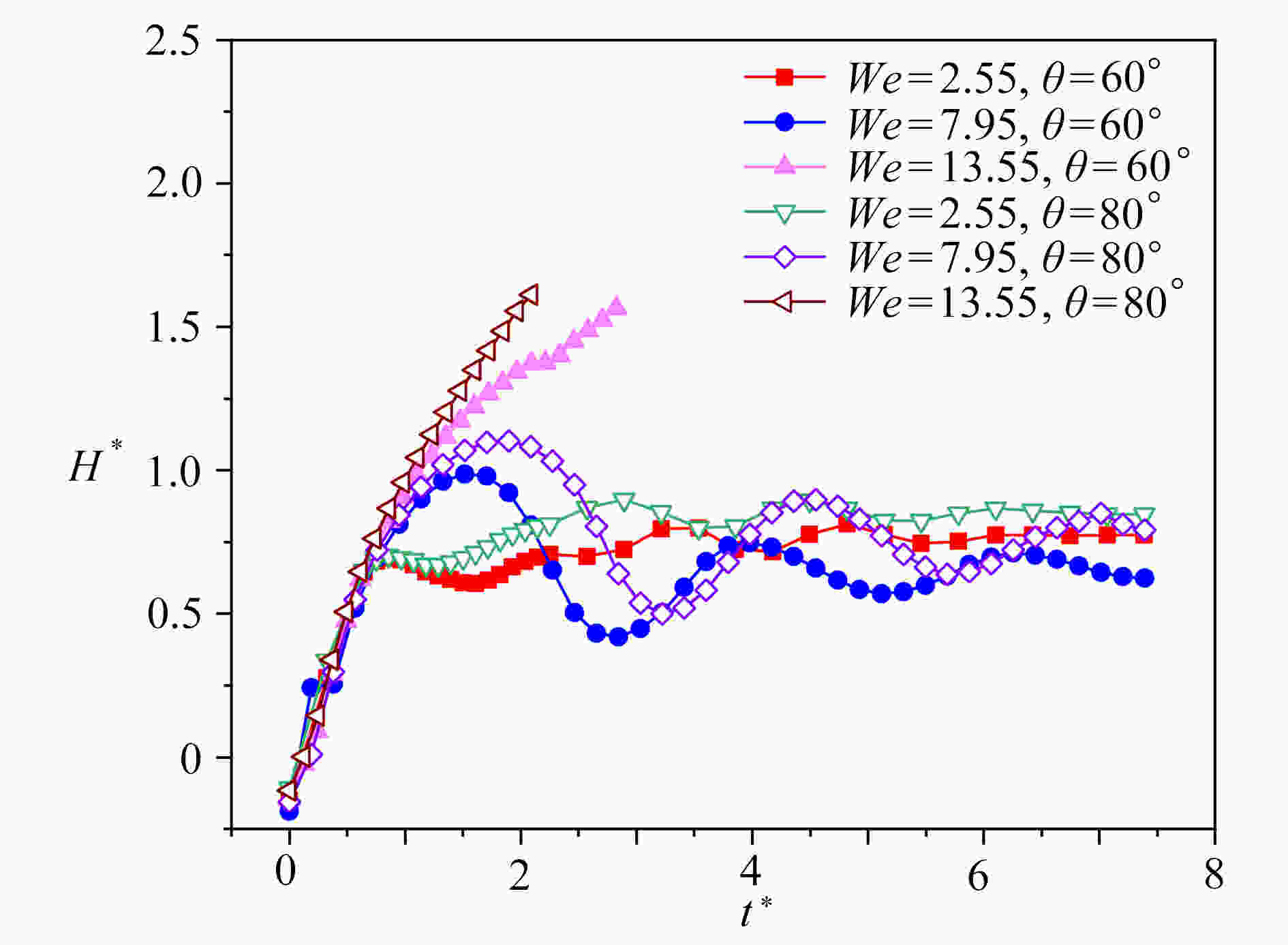
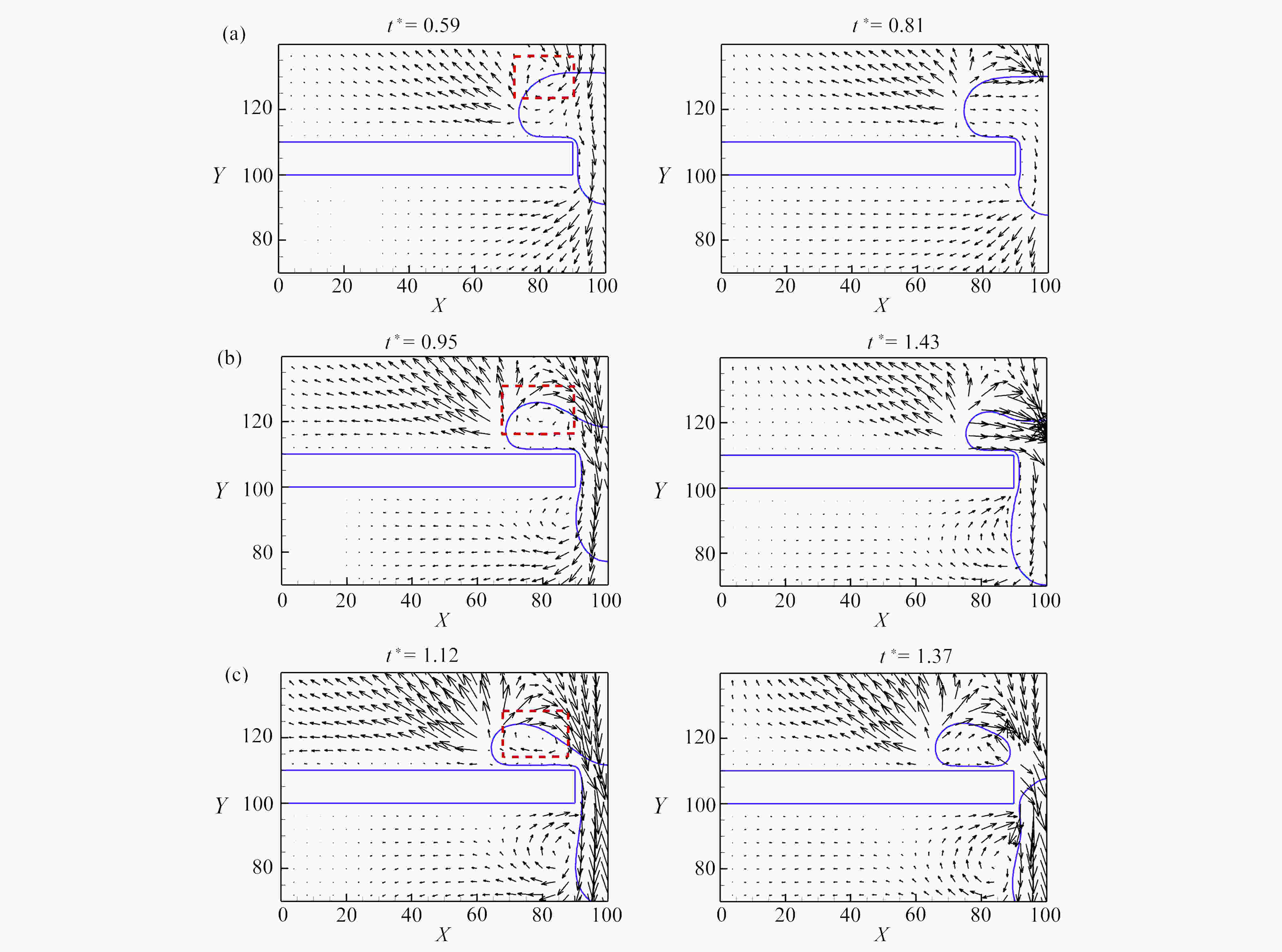
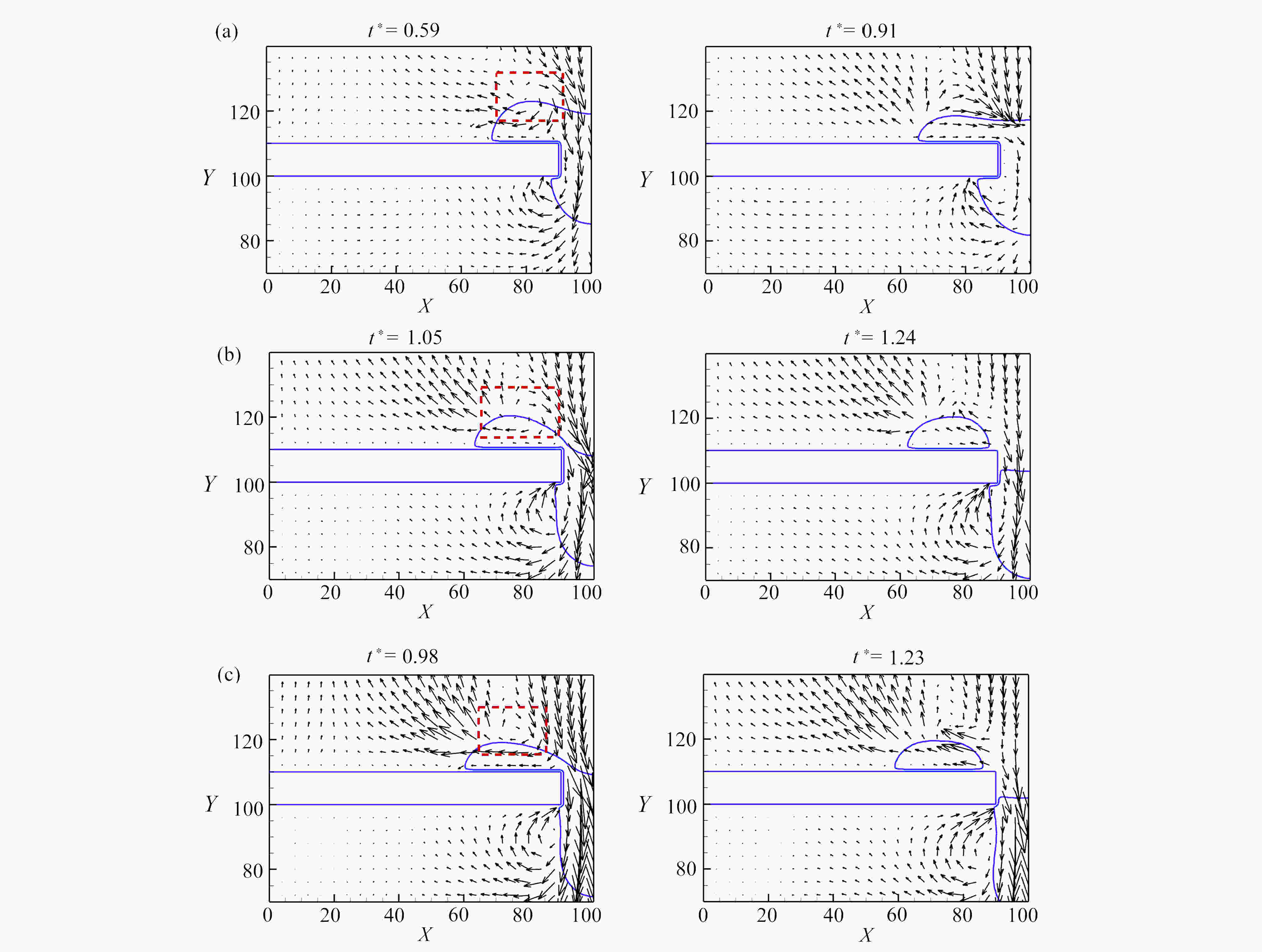
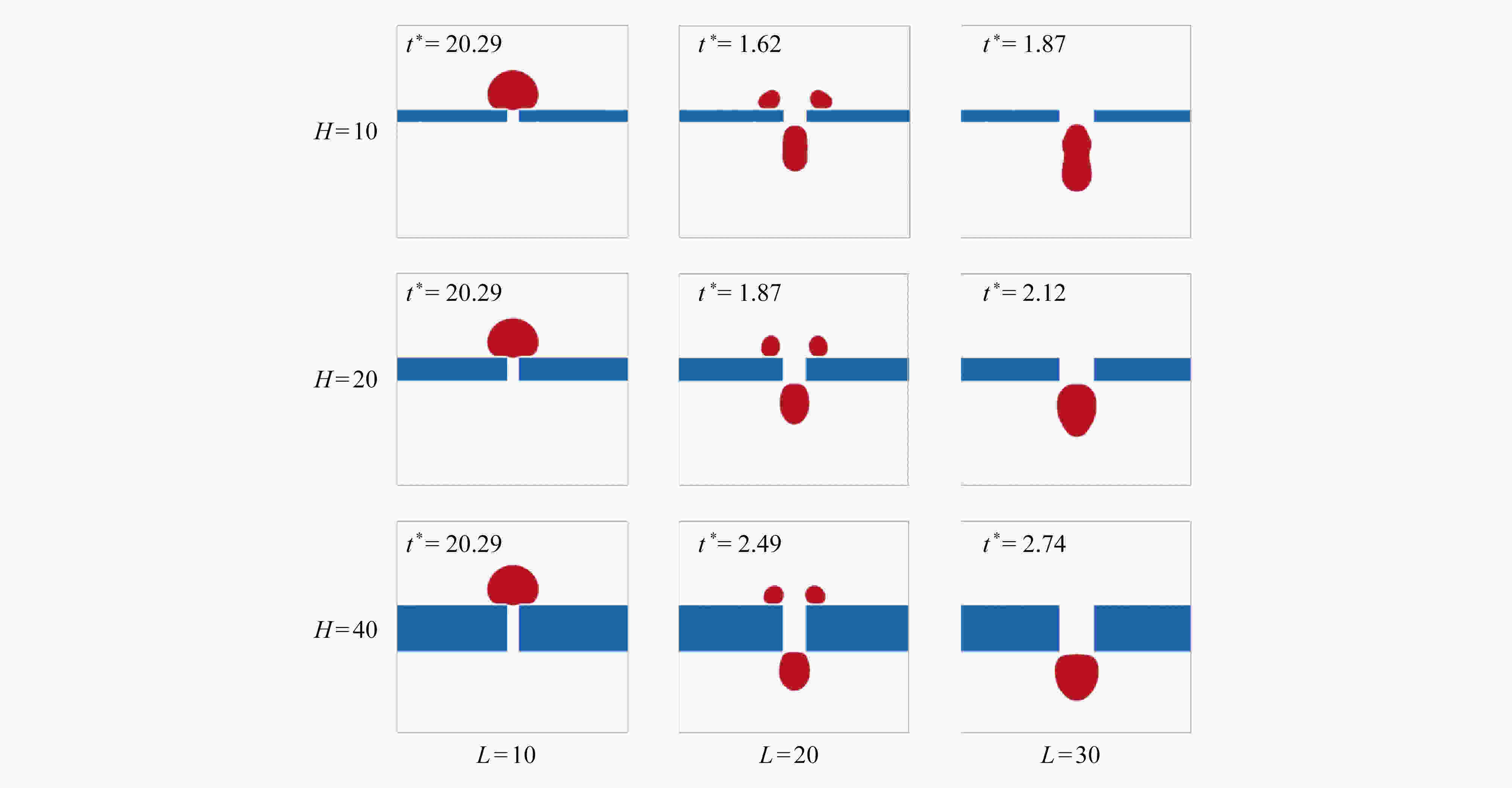
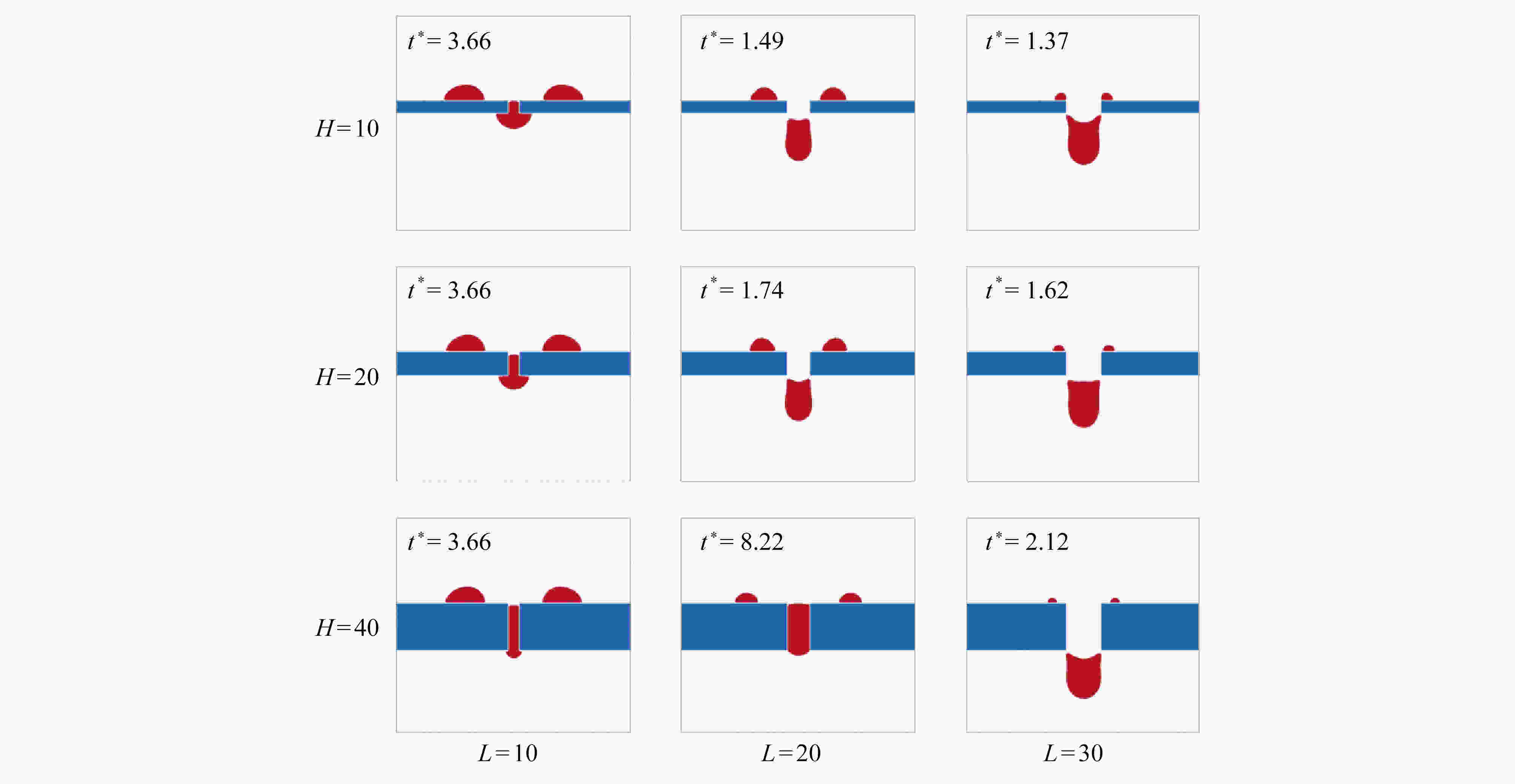
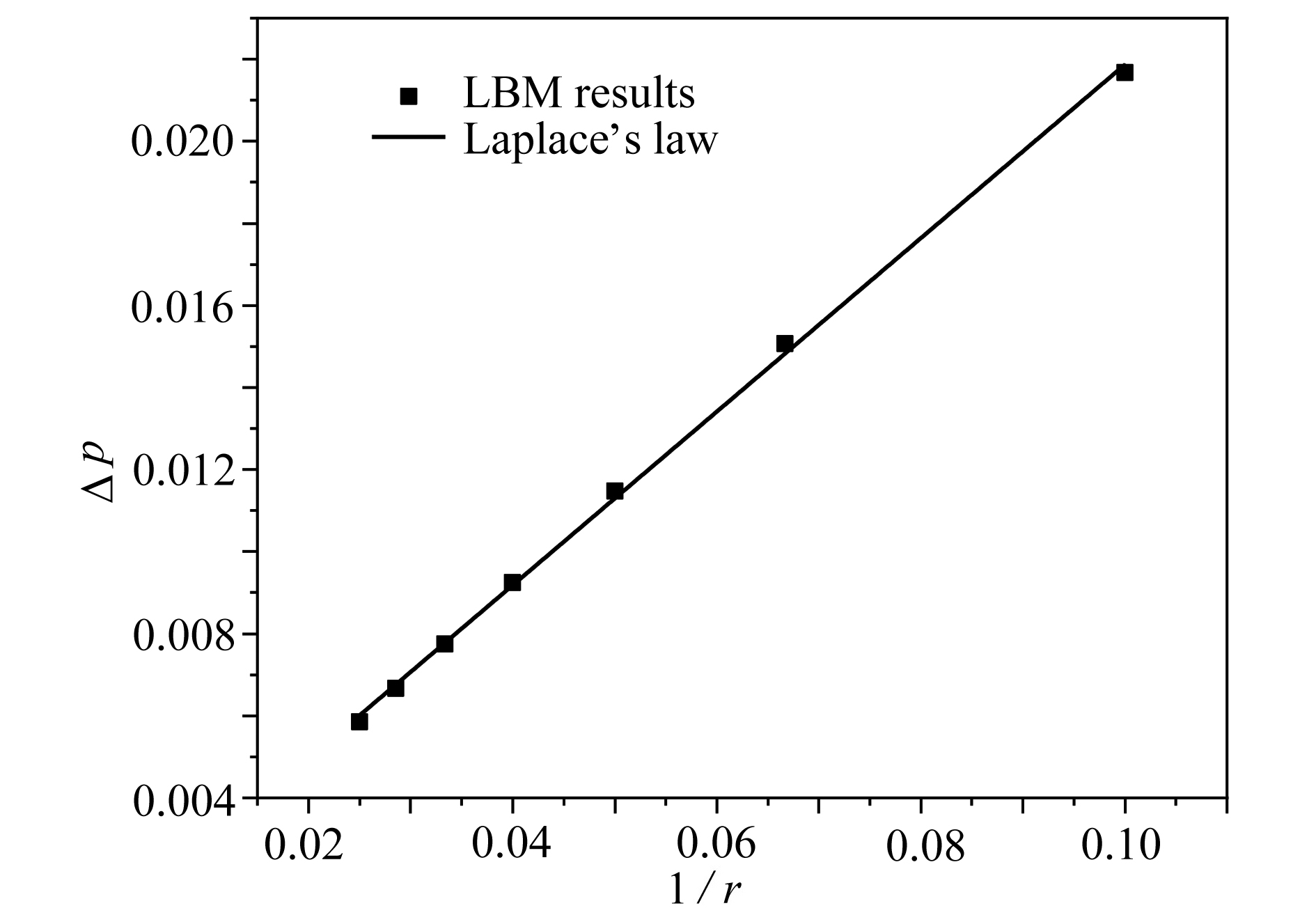
基于格子Boltzmann方法，对液滴撞击不同湿润性节流孔板表面进行了数值模拟。主要研究了在液滴撞击过程中，Weber数（We）、孔板表面湿润性和孔板尺寸对液滴通过孔板时不同状态的影响。数值模拟结果表明：孔板为亲水特性时，在较低We下，液滴不会与孔板表面脱离，而是附着在孔板下表面，并且在毛细作用下液滴会在孔道中上升一段距离，形成液塞现象，在较高We下，液滴会穿过孔板，并发生破裂现象；孔板为疏水特性时，在较低We下，液滴无法穿过孔板，且无法迁移至下表面，最终稳定在孔板孔道上，在较高We下，液滴能穿过孔板，穿过时会发生破裂，孔板上表面会残留液滴。改变孔板尺寸发现，在较小的孔板孔径以及较厚的孔板厚度下，液滴不易通过。
-
关键词:
- 格子Boltzmann方法 /
- 液滴撞击 /
- 节流孔板 /
- 亲疏水表面
Abstract:Based on the lattice Boltzmann method, the numerical simulation of droplet impacting on orifice plates with different wettabilities was carried out. The effects of the Weber number (We), the wettability of the orifice surface and the orifice size on different states of droplets passing through orifice plates during impacts were studied. The numerical simulation results show that, different phenomena will occur in the processes of droplets impacting on the orifice plates. If the orifice plate is hydrophilic, the droplet will not detach from the orifice plate surface, but adhere to the lower surface of the orifice plate for a relatively low We number, and then the droplet will rise for a certain distance in the orifice channel under the action of capillarity, forming the liquid plugging phenomenon. For relatively high We numbers, droplets will pass through the orifice plates and rupture will occur. If the orifice plate is hydrophobic, the droplet will not pass through the orifice plate and migrate to the lower surface for a relatively low We number, and will finally stabilize in the orifice channel. For higher We numbers, droplets will pass through the orifice plates, and then break up, leaving droplet remains on the surfaces of the orifice plates. For various orifice sizes, the droplet will be more difficult to pass through the plate for a smaller orifice size or a lager orifice plate thickness.
-
图 4 We对液滴撞击疏水孔板表面的影响(
$ \theta {\text{ = }}{120^ \circ } $ ，L=20，H=10)：(a) We=2.55；(b) We=7.95；(c) We=13.55Figure 4. Effects of the We number of droplets impacting on hydrophobic orifice surface (
$ \theta {\text{ = }}{120^ \circ } $ ，L=20，H=10)：(a) We=2.55；(b) We=7.95；(c) We=13.55
图 5 We对液滴撞击疏水孔板表面的影响(
$ \theta {\text{ = }}{160^ \circ } $ ，L=20，H=10)：(a) We=2.55；(b) We=7.95；(c) We=13.55Figure 5. Effects of the We number of droplets impacting on hydrophobic orifice surface (
$ \theta {\text{ = }}{160^ \circ } $ , L=20，H=10): (a) We=2.55; (b) We=7.95; (c) We=13.55
图 8 We对液滴撞击亲水孔板表面的影响(
$ \theta {\text{ = }}{60^ \circ } $ ，L=20，H=10)：(a) We=2.55；(b) We=7.95；(c) We=13.55Figure 8. Effects of the We number of droplets impacting on hydrophilic orifice surface (
$ \theta {\text{ = }}{60^ \circ } $ ，L=20，H=10)：(a) We=2.55；(b) We=7.95；(c) We=13.55
图 9 We对液滴撞击亲水孔板表面的影响(
$ \theta {\text{ = }}{80^ \circ } $ ，L=20，H=10)：(a) We=2.55；(b) We=7.95；(c) We=13.55Figure 9. Effects of the We number of droplets impacting on hydrophilic orifice surface (
$ \theta {\text{ = }}{80^ \circ } $ , L=20, H=10): (a) We=2.55; (b) We=7.95; (c) We=13.55
图 12 疏水孔板液滴的速度场(
$ \theta {\text{ = }}{160^ \circ } $ ，L=20，H=10)：(a) We=2.55；(b) We=7.95；(c) We=13.55Figure 12. The velocity fields of the droplets on the hydrophobic plates (
$ \theta {\text{ = }}{160^ \circ } $ ，L=20，H=10)：(a) We=2.55；(b) We=7.95；(c) We=13.55
图 13 亲水孔板液滴的速度场(
$ \theta {\text{ = }}{80^ \circ } $ ，L=20，H=10)：(a) We =2.55；(b) We =7.95；(c) We =13.55Figure 13. The velocity fields inside the droplets on the hydrophilic plates(
$ \theta {\text{ = }}{80^ \circ } $ ，L=20，H=10)：(a) We=2.55；(b) We=7.95；(c) We=13.55
图 14 液滴撞击不同尺寸疏水节流孔板(We=13.55，
$ \theta {\text{ = }}{160^ \circ } $ )Figure 14. Droplets impacting on different-size hydrophobic orifice plates (We=13.55，
$ \theta {\text{ = }}{160^ \circ } $ ) -
[1] CHANDRA S, MOSTAGHIMI J. Spray impingement fundamentals[M]//Metal Sprays and Spray Deposition. HENEIN H, UHLENWINKEL V, FRITSCHING U, eds. Springer, 2017. [2] BURGUÉS-CEBALLOS I, STELLA M, LACHARMOISE P, et al. Towards industrialization of polymer solar cells: material processing for upscaling[J]. Journal of Materials Chemistry A, 2014, 2(42): 17711-17722. doi: 10.1039/C4TA03780D [3] SON Y, KIM C, YANG D H, et al. Spreading of an inkjet droplet on a solid surface with a controlled contact angle at low Weber and Reynolds numbers[J]. Langmuir, 2008, 24(6): 2900-2907. doi: 10.1021/la702504v [4] WORTHINGTON A. On the forms assumed by drops of liquids falling vertically on a horizontal plate[J]. Proceedings of the Royal Society of London, 1876, 25: 261-272. [5] WORTHINGTON A. A second paper on the forms assumed by drops of liquids falling vertically on a horizontal plate[J]. Proceedings of the Royal Society of London, 1876, 25: 498-503. [6] RIOBOO R, TROPEA C, MARENGO M. Outcomes from a drop impact on solid surfaces[J]. Atomization and Sprays, 2001, 11(2): 155-165. [7] WANG F C, FENG J T, ZHAO Y P. The head-on colliding process of binary liquid droplets at low velocity: high-speed photography experiments and modeling[J]. Journal of Colloid and Interface Science, 2008, 326(1): 196-200. doi: 10.1016/j.jcis.2008.07.002 [8] 毕菲菲, 郭亚丽, 沈胜强, 等. 液滴撞击固体表面铺展特性的实验研究[J]. 物理学报, 2012, 61(18): 295-300. (BI Feifei, GUO Yali, SHEN Shengqiang, et al. Experimental study of spread characteristics of droplet impacting solid surface[J]. Acta Physica Sinica, 2012, 61(18): 295-300.(in Chinese) [9] LORENCEAU É, QUÉRÉ D. Drops impacting a sieve[J]. Journal of Colloid and Interface Science, 2003, 263(1): 244-249. [10] RICHARD D, QUÉRÉ D. Bouncing water drops[J]. Europhysics Letters, 2000, 50(6): 769-775. doi: 10.1209/epl/i2000-00547-6 [11] PAN K L, CHOU P C, TSENG Y J. Binary droplet collision at high Weber number[J]. Physical Review E: Statistical, Nonlinear, and Soft Matter Physics, 2009, 80(3): 036301. [12] SHEN Y, TAO J, WANG G, et al. Bioinspired fabrication of hierarchical-structured superhydrophobic surfaces to understand droplet bouncing dynamics for enhancing water repellency[J]. The Journal of Physical Chemistry C: Nanomaterials & Interfaces, 2018, 122(13): 7312-7320. [13] BUSSMANN M, MOSTAGHIMI J, CHANDRA S. On a three-dimensional volume tracking model of droplet impact[J]. Physics of Fluids, 1999, 11(6): 1406-1417. doi: 10.1063/1.870005 [14] PASANDIDEH-FARD M, QIAO Y M, CHANDRA S, et al. Capillary effects during droplet impact on a solid surface[J]. Physics of Fluids, 1996, 8(3): 650-659. doi: 10.1063/1.868850 [15] RUSSO A, ICARDI M, ELSHARKAWY M, et al. Numerical simulation of droplet impact on wettability-patterned surfaces[J]. Physical Review Fluids, 2020, 5(7): 074002. doi: 10.1103/PhysRevFluids.5.074002 [16] 何雅玲, 李庆, 王勇, 等. 格子Boltzmann方法的工程热物理应用[J]. 科学通报, 2009, 54(18): 2638-2656. (HE Yaling, LI Qing, WANG Yong, et al. Lattice Boltzmann method and its applications in engineering thermophysics[J]. Chinese Science Bulletin, 2009, 54(18): 2638-2656.(in Chinese) doi: 10.1360/csb2009-54-18-2638 [17] 郭照立, 郑楚光, 李青, 等. 流体动力学的格子Boltzmann方法[M]. 武汉: 湖北科学技术出版社, 2002.GUO Zhaoli, ZHENG Chuguang, LI Qing, et al. Lattice Boltzmann Method for Hydrodynamics[M]. Wuhan: Hubei Science & Technology Press, 2002. (in Chinese) [18] WANG D, TAN D S, KHOO B C, et al. A lattice Boltzmann modeling of viscoelastic drops’ deformation and breakup in simple shear flows[J]. Physics of Fluids, 2020, 32(12): 123101. doi: 10.1063/5.0031352 [19] 谢驰宇, 张建影, 王沫然. 液滴在固体平表面上均匀蒸发过程的格子Boltzmann模拟[J]. 应用数学和力学, 2014, 35(3): 247-253. (XIE Chiyu, ZHANG Jianying, WANG Moran. Lattice Boltzmann simulation of droplet evaporation on flat solid surface[J]. Applied Mathematics and Mechanics, 2014, 35(3): 247-253.(in Chinese) doi: 10.3879/j.issn.1000-0887.2014.03.002 [20] 许友生, 刘慈群, 俞慧丹. 多孔介质中两相驱离的格子Boltzmann模型新研究[J]. 应用数学和力学, 2002, 23(4): 353-358. (XU Yousheng, LIU Ciqun, YU Huidan. New studying of lattice Boltzmann method for two phase driven in porous media[J]. Applied Mathematics and Mechanics, 2002, 23(4): 353-358.(in Chinese) doi: 10.3321/j.issn:1000-0887.2002.04.004 [21] GUNSTENSEN A K, ROTHMAN D H, ZALESKI S, et al. Lattice Boltzmann model of immiscible fluids[J]. Physical Review A, 1991, 43(8): 4320-4327. doi: 10.1103/PhysRevA.43.4320 [22] SHAN X, CHEN H. Lattice Boltzmann model for simulating flows with multiple phases and components[J]. Physical Review E, 1993, 47(3): 1815-1819. doi: 10.1103/PhysRevE.47.1815 [23] SWIFT M R, ORLANDINI E, OSBORN W R, et al. Lattice Boltzmann simulations of liquid-gas and binary fluid systems[J]. Physical Review E, 1996, 54(5): 5041-5052. doi: 10.1103/PhysRevE.54.5041 [24] HE X, CHEN S, ZHANG R. A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh-Taylor instability[J]. Journal of Computational Physics, 1999, 152(2): 642-663. doi: 10.1006/jcph.1999.6257 [25] HE X, SHAN X, DOOLEN G D. Discrete Boltzmann equation model for nonideal gases[J]. Physical Review E, 1998, 57(1): R13-R16. doi: 10.1103/PhysRevE.57.R13 [26] DALGAMONI H N, YONG X. Axisymmetric lattice Boltzmann simulation of droplet impact on solid surfaces[J]. Physical Review E, 2018, 98(1): 013102. doi: 10.1103/PhysRevE.98.013102 [27] CHENG Z, BA Y, SUN J, et al. A numerical study of droplet dynamic behaviors on a micro-structured surface using a three dimensional color-gradient lattice Boltzmann model[J]. Soft Matter, 2018, 14(5): 837-847. doi: 10.1039/C7SM02078C [28] GUPTA A, KUMAR R. Simulation of droplet flows using lattice Boltzmann method[C]//ASME 2008 6th International Conference on Nanochannels, Microchannels, and Minichannels. Darmstadt, Germany, 2008. [29] ZHAO W D, ZHANG Y, XU B. An improved pseudopotential multi-relaxation-time lattice Boltzmann model for binary droplet collision with large density ratio[J]. Fluid Dynamics Research, 2019, 51(2): 025510. doi: 10.1088/1873-7005/aae443 [30] GONG S, CHENG P. Numerical investigation of droplet motion and coalescence by an improved lattice Boltzmann model for phase transitions and multiphase flows[J]. Computers & Fluids, 2012, 53: 93-104. [31] XIONG W, CHENG P. 3D lattice Boltzmann simulation for a saturated liquid droplet at low Ohnesorge numbers impact and breakup on a solid surface surrounded by a saturated vapor[J]. Computers & Fluids, 2018, 168: 130-143. [32] QIAN Y H, D’HUMIERES D, LALLEMAND P. Lattice BGK models for Navier-Stokes equation[J]. Europhysics Letter, 1992, 17(6): 479. doi: 10.1209/0295-5075/17/6/001 [33] KUPERSHTOKH A L, MEDVEDEV D A. Lattice Boltzmann equation method in electrohydrodynamic problems[J]. Journal of Electrostatics, 2006, 64(7/9): 581-585. doi: 10.1016/j.elstat.2005.10.012 [34] CHEN L, KANG Q, ROBINSON B A, et al. Pore-scale modeling of multiphase reactive transport with phase transitions and dissolution-precipitation processes in closed systems[J]. Physical Review E, 2013, 87(4): 043306. doi: 10.1103/PhysRevE.87.043306 [35] CLANET C, BÉGUIN C, RICHARD D, et al. Maximal deformation of an impacting drop[J]. Journal of Fluid Mechanics, 2004, 517: 199-208. doi: 10.1017/S0022112004000904 [36] HAGHANI R, RAHIMIAN M H. Four different types of a single drop dripping down a hole under gravity by lattice Boltzmann method[J]. Journal of Computational Applied Mechanics, 2016, 47(1): 89-98. [37] HAGHANI R, RAHIMIAN M H, TAGHILOU M. LBM simulation of a droplet dripping down a hole[J]. Engineering Applications of Computational Fluid Mechanics, 2013, 7(4): 461-470. doi: 10.1080/19942060.2013.11015485 [38] YUAN X, CHAI Z, SHI B. Dynamic behavior of droplet through a confining orifice: a lattice Boltzmann study[J]. Computers & Mathematics With Applications, 2019, 77(10): 2640-2658. [39] FAKHARI A, RAHIMIAN M H. Simulation of falling droplet by the lattice Boltzmann method[J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14(7): 3046-3055. doi: 10.1016/j.cnsns.2008.10.017 -
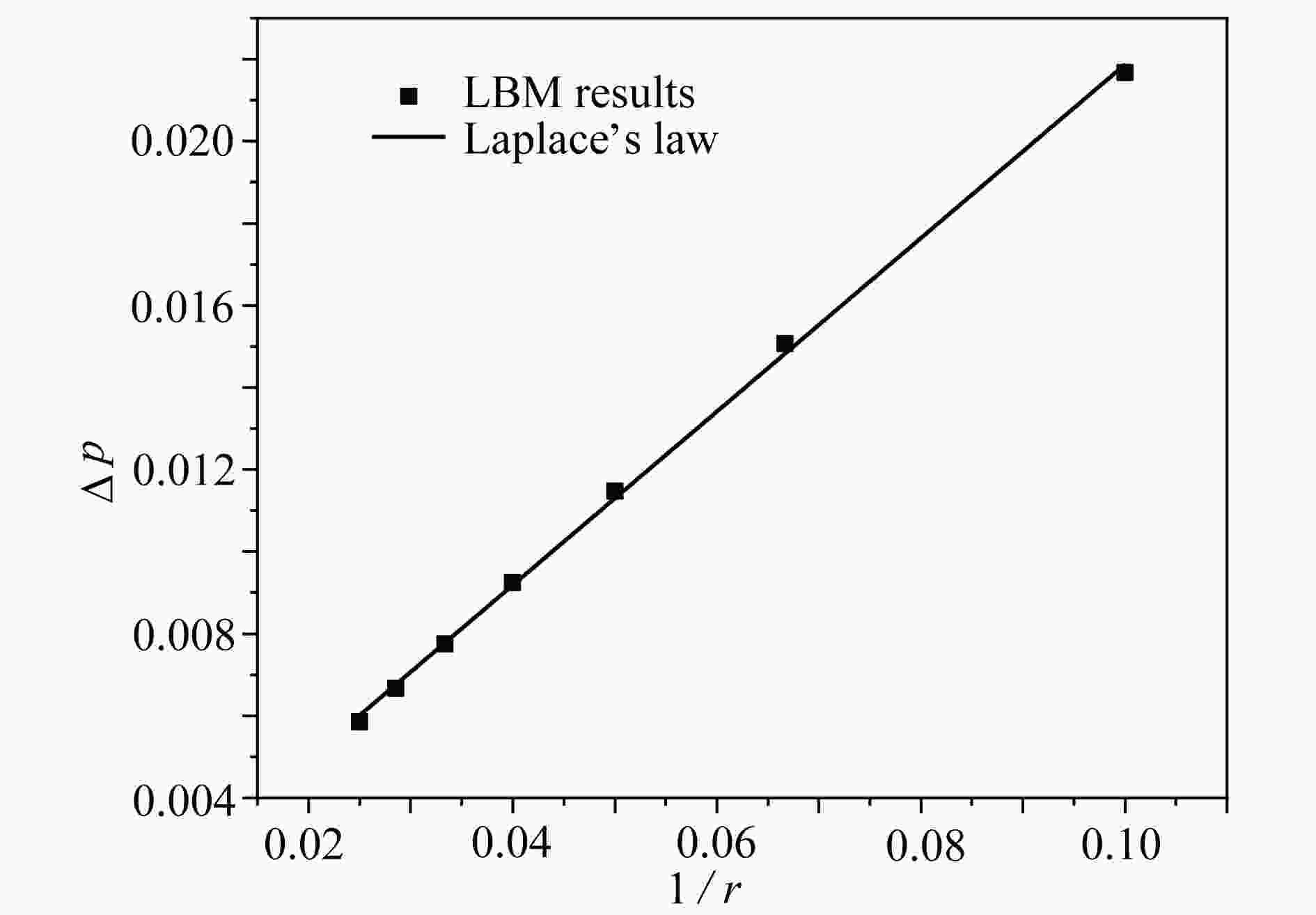
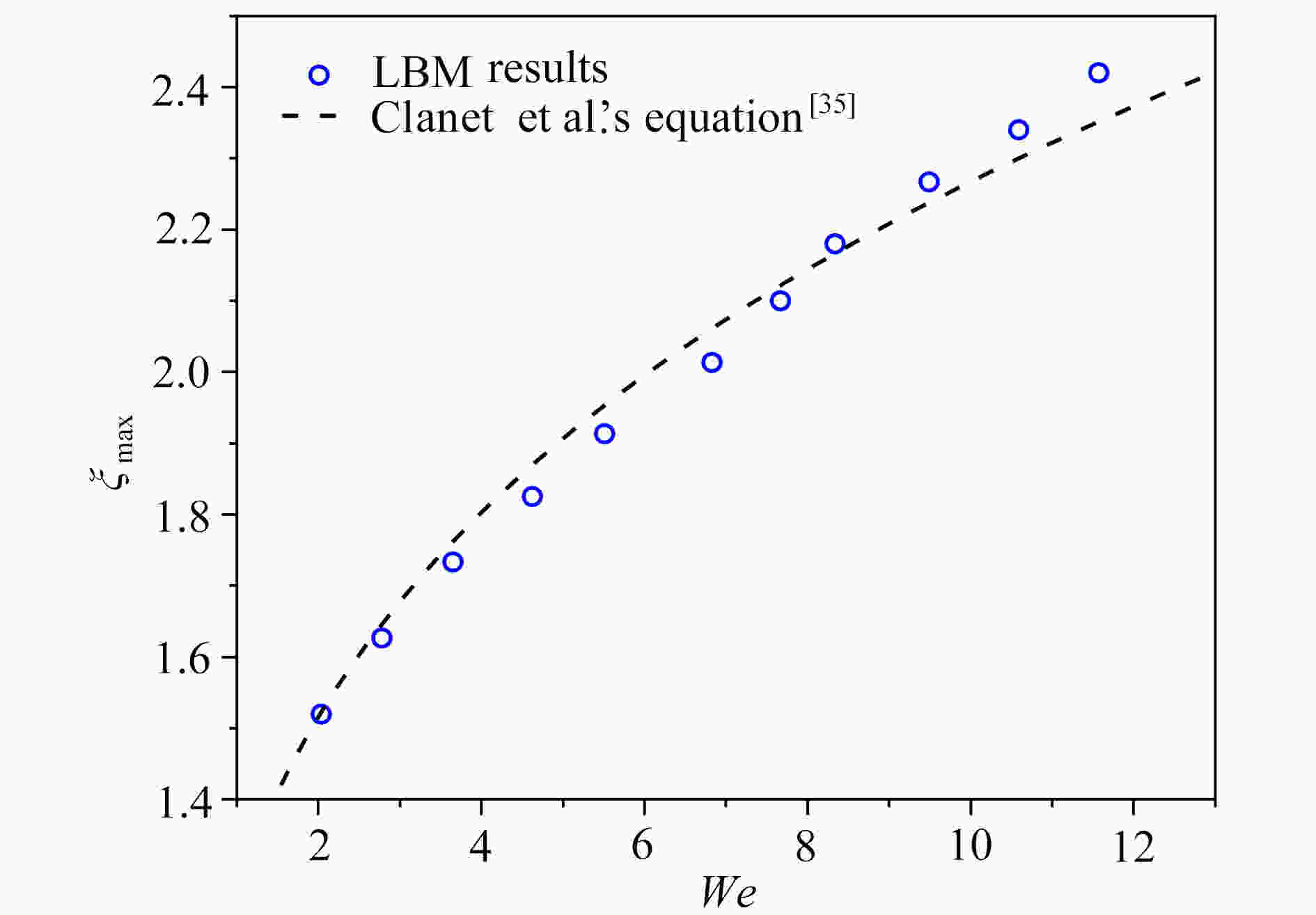
下载:
计量
- 文章访问数: 696
- HTML全文浏览量: 310
- PDF下载量: 53
- 被引次数: 0
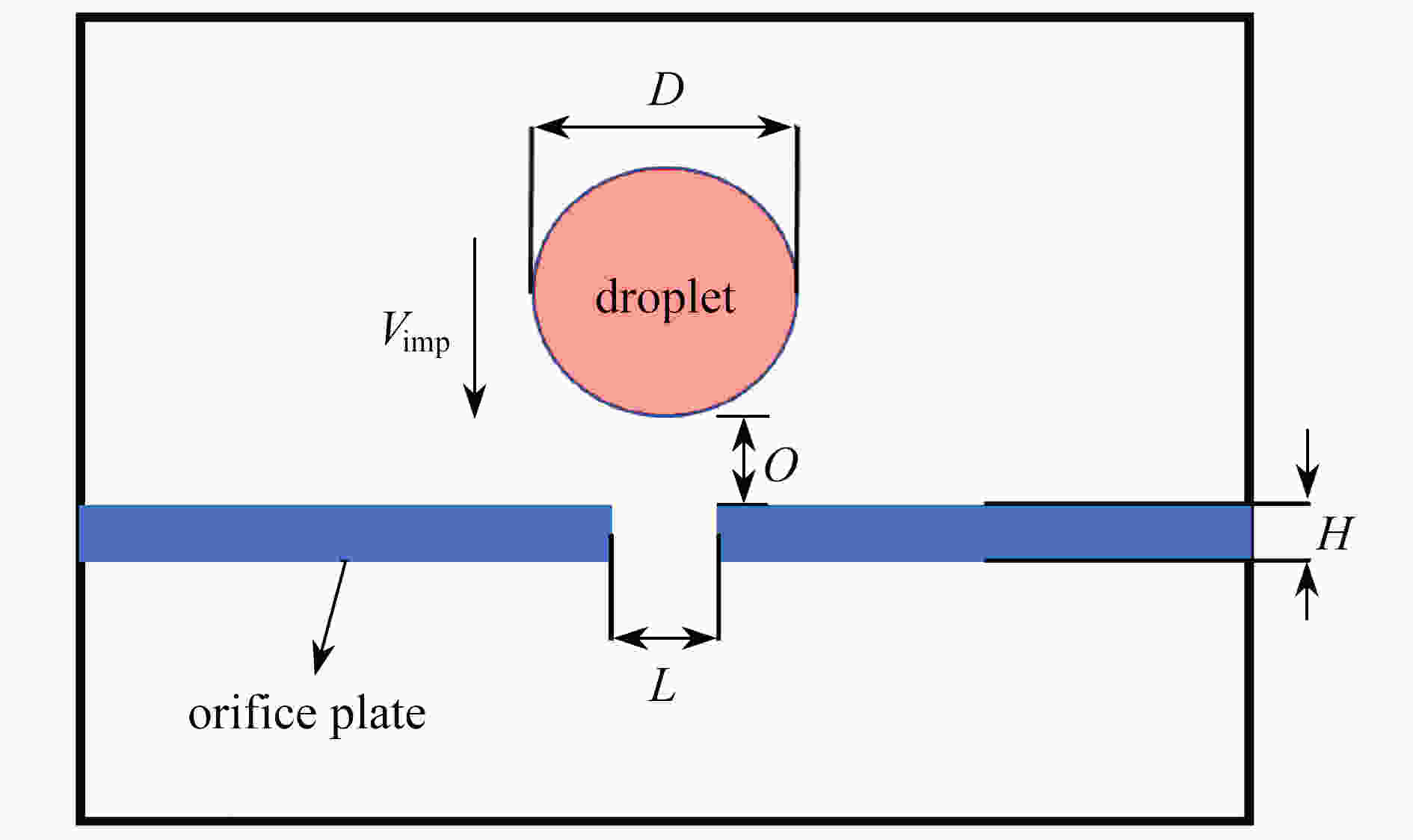
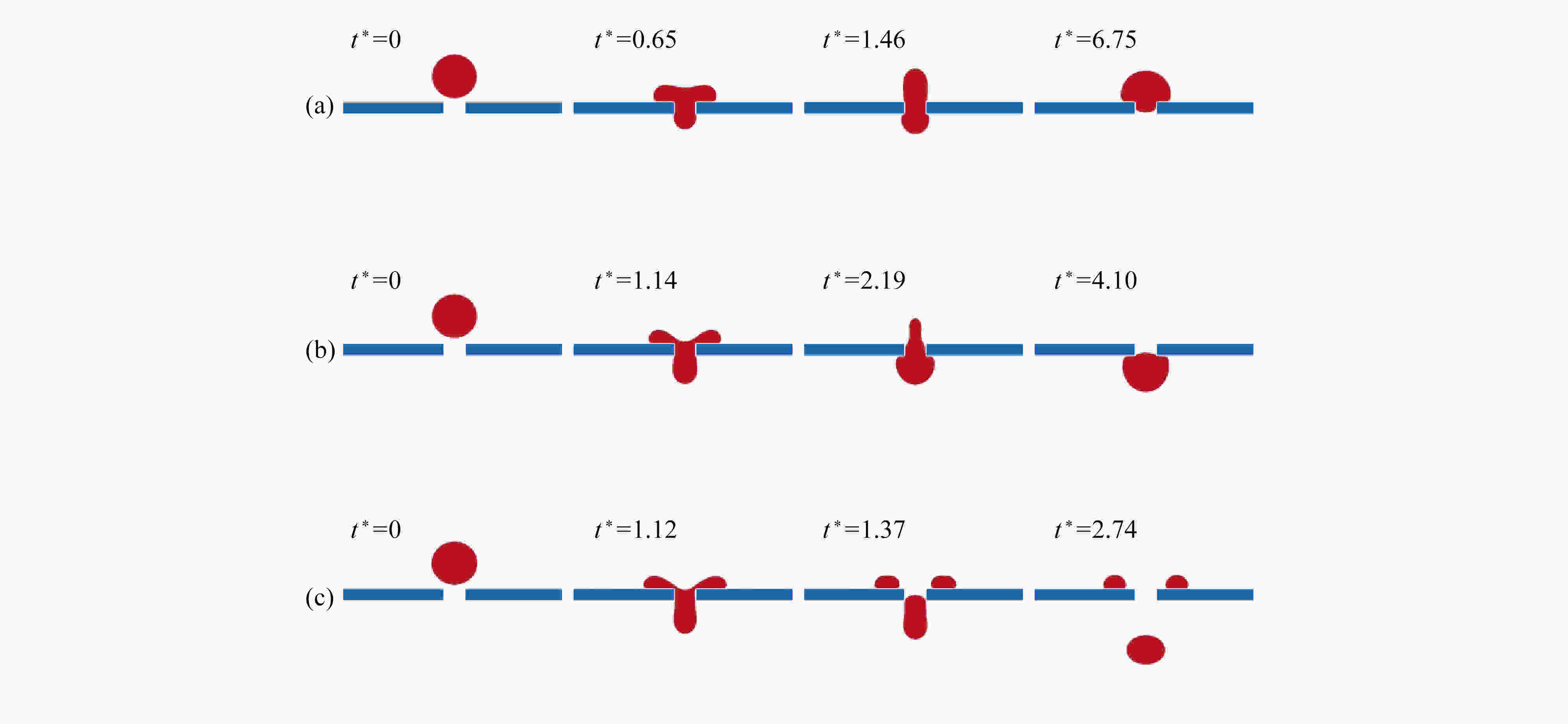
渝公网安备50010802005915号