Numerical Analysis on Effects of Wall Structures on Bubble Groups
doi: 10.21656/1000-0887.420041
壁面结构对三维可压缩气泡群影响的数值模拟研究
-
摘要:
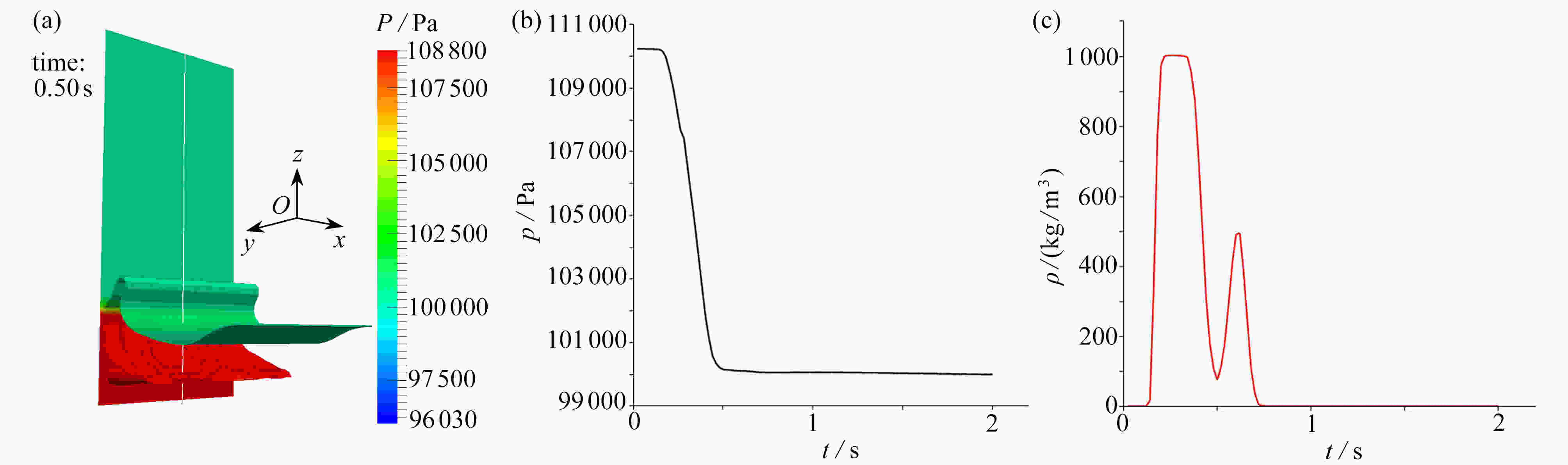
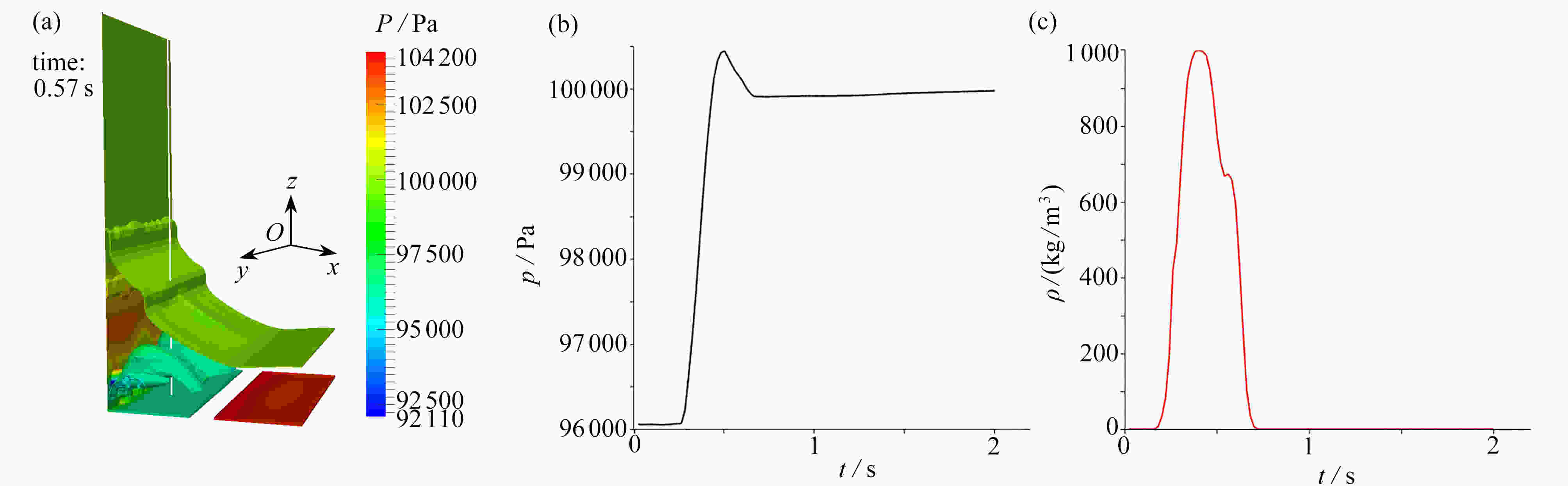
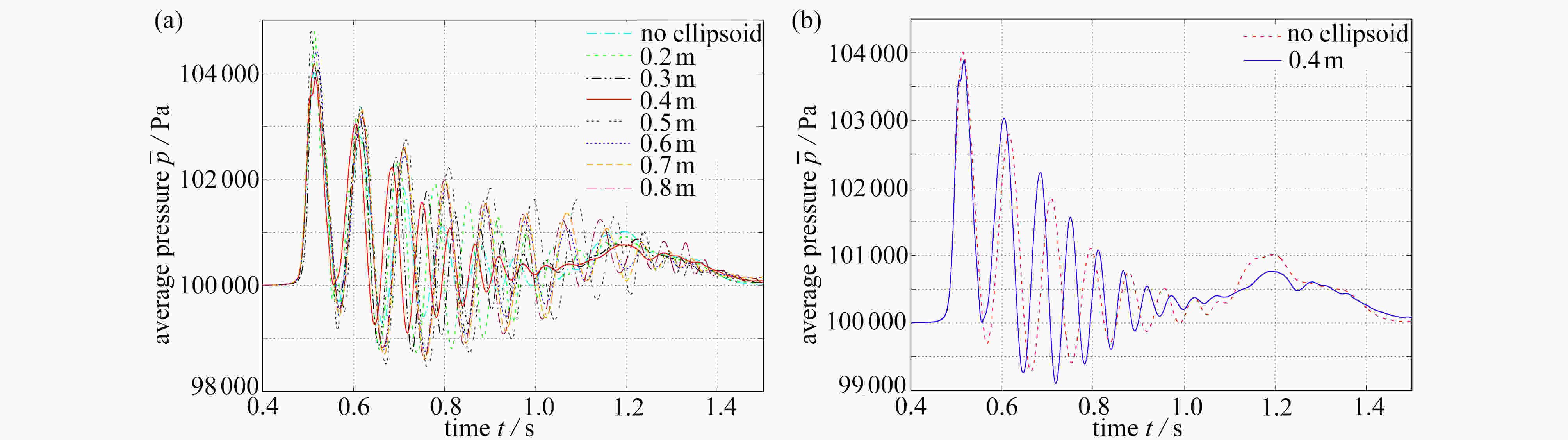
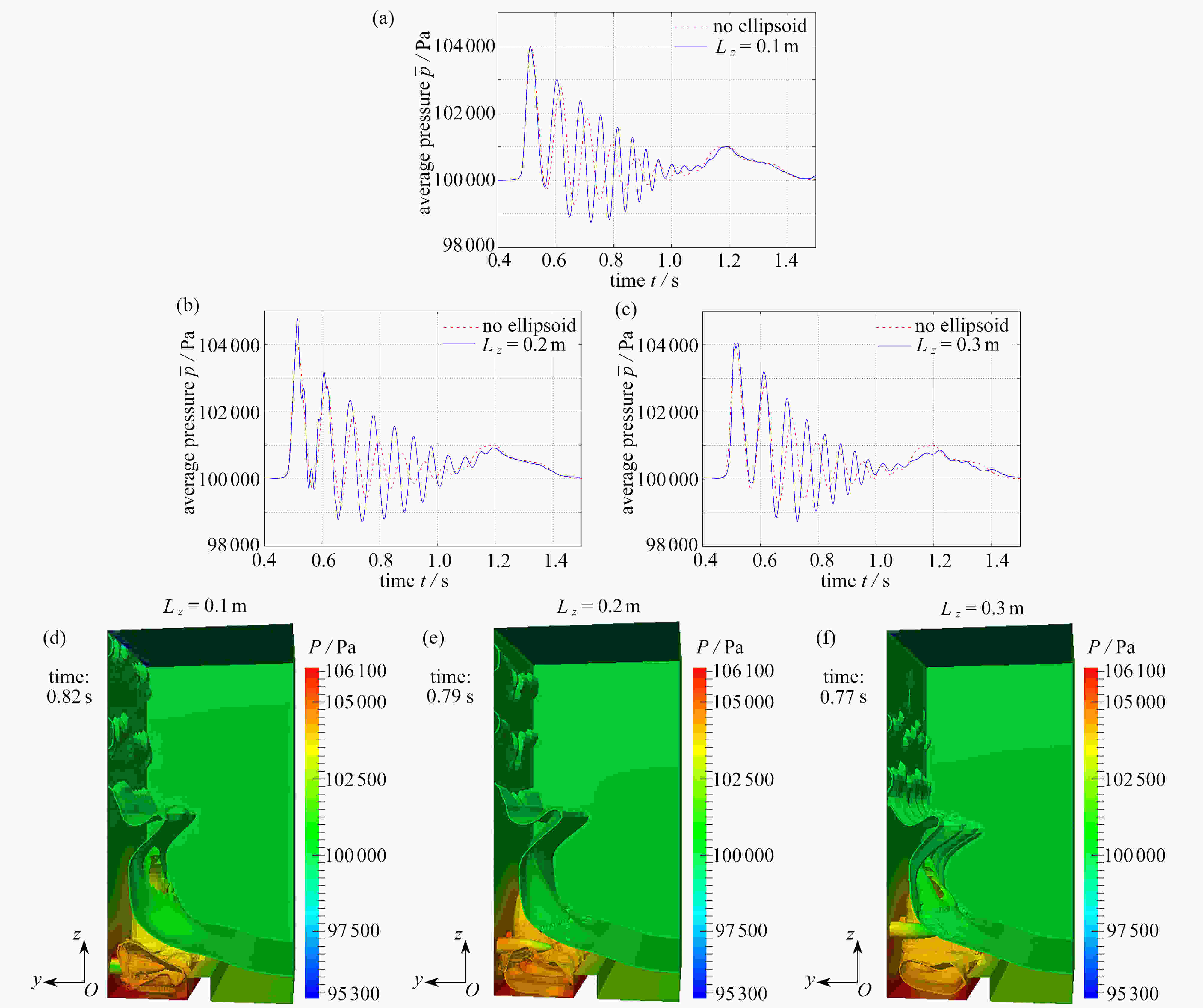
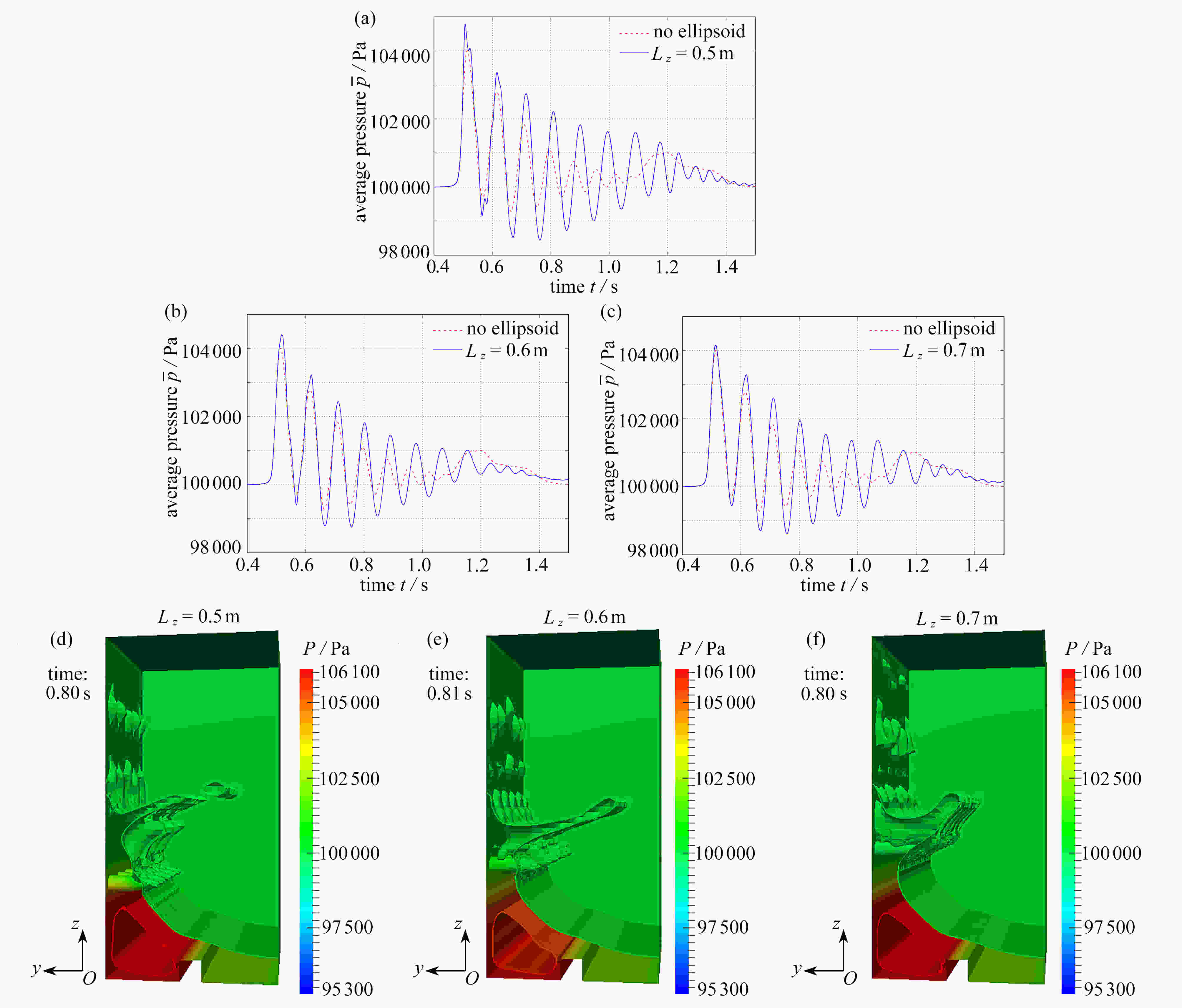
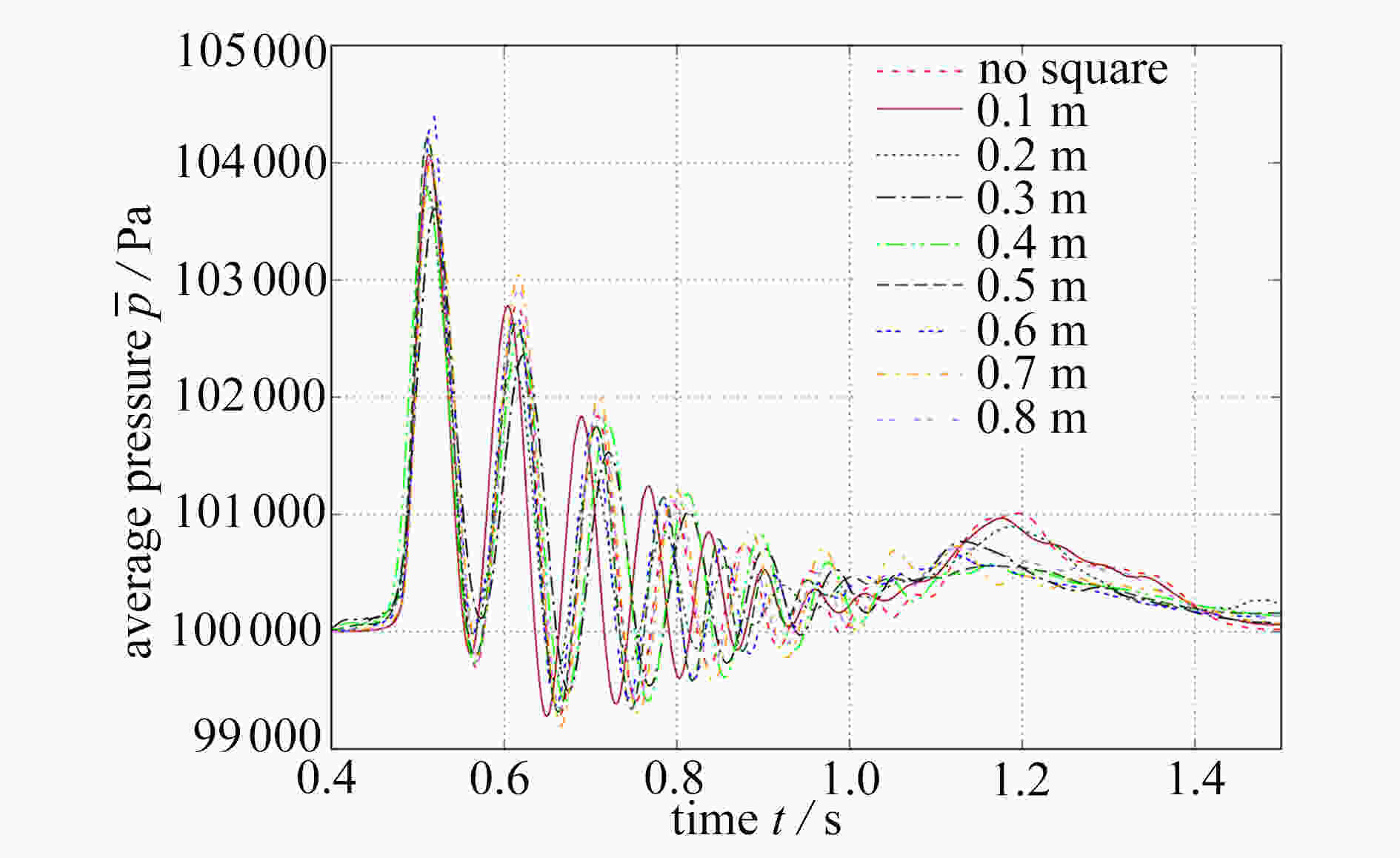
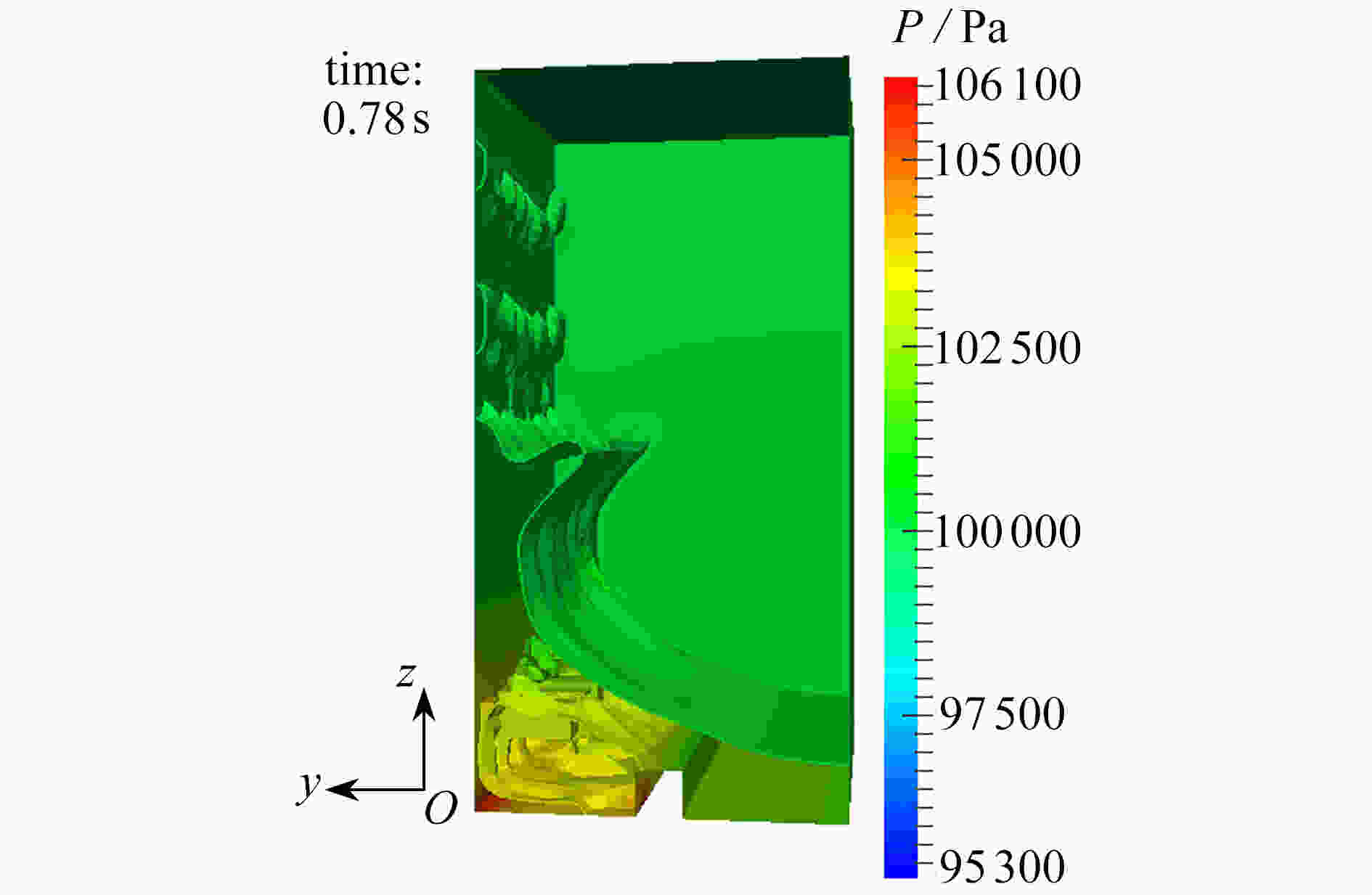
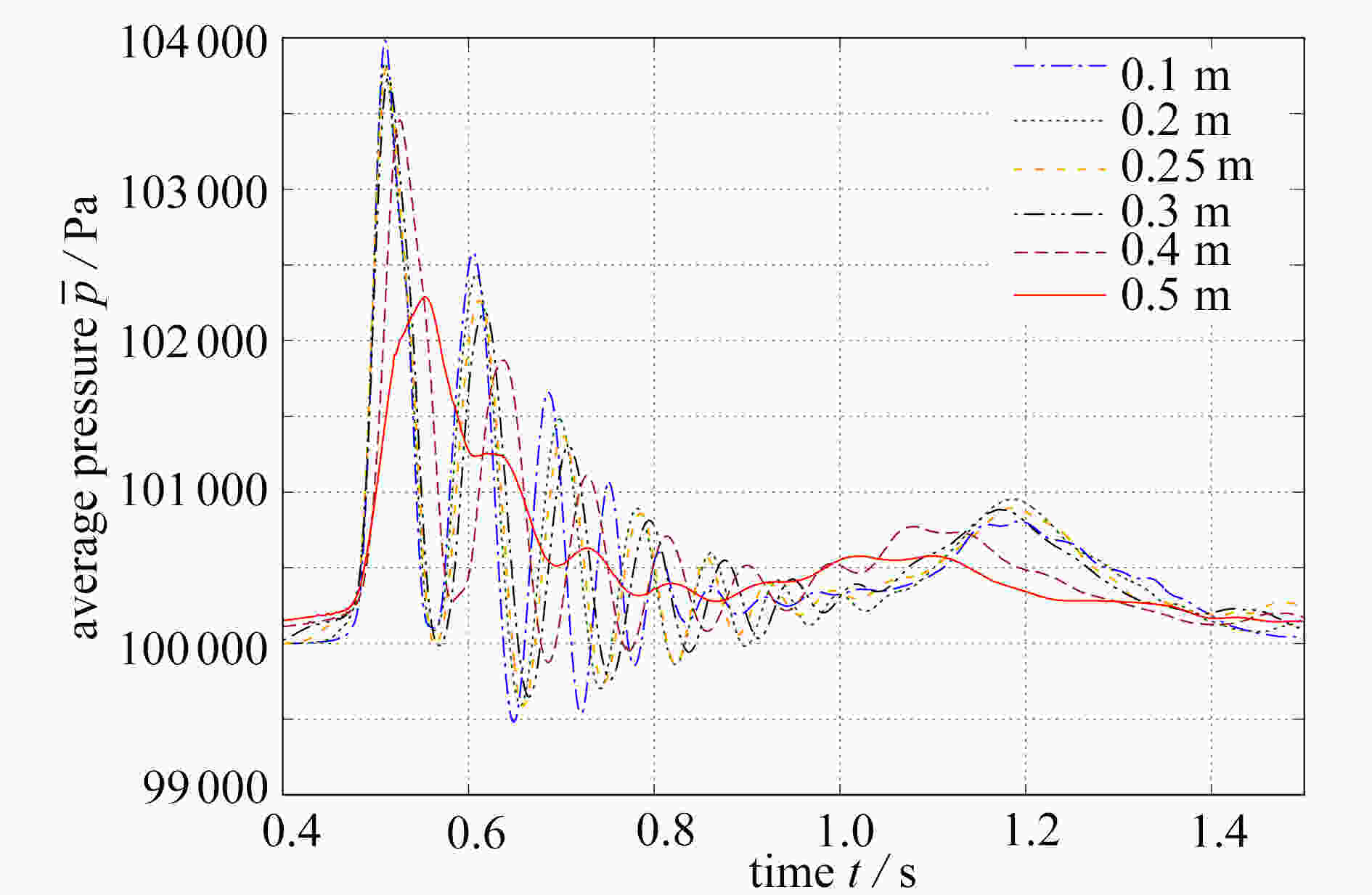
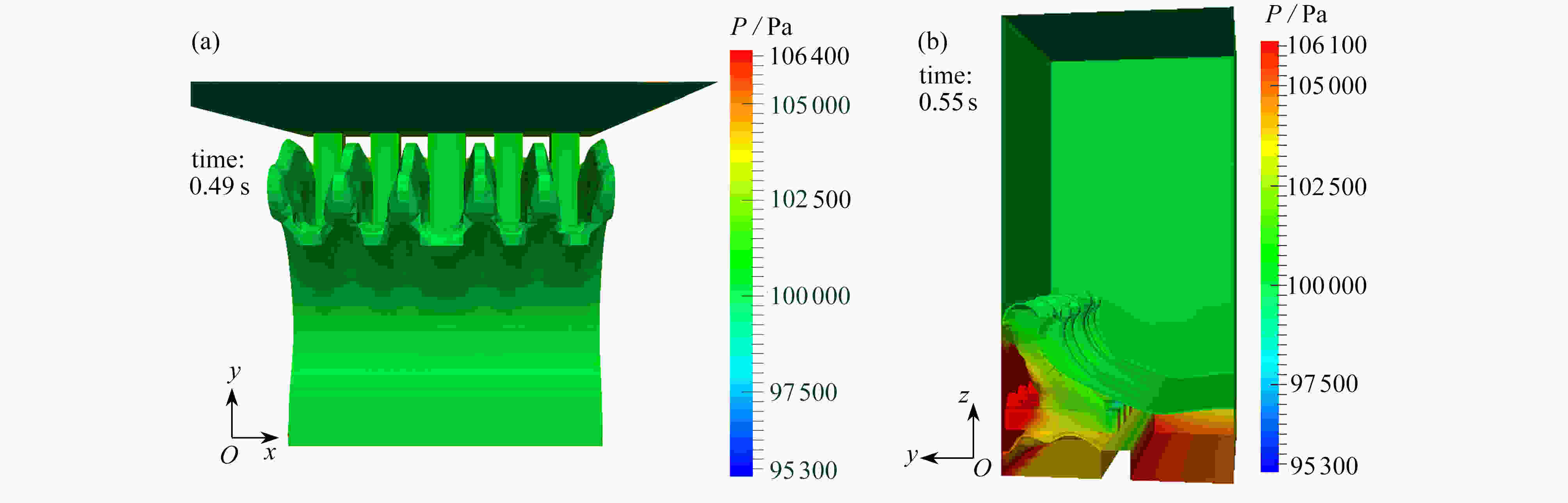
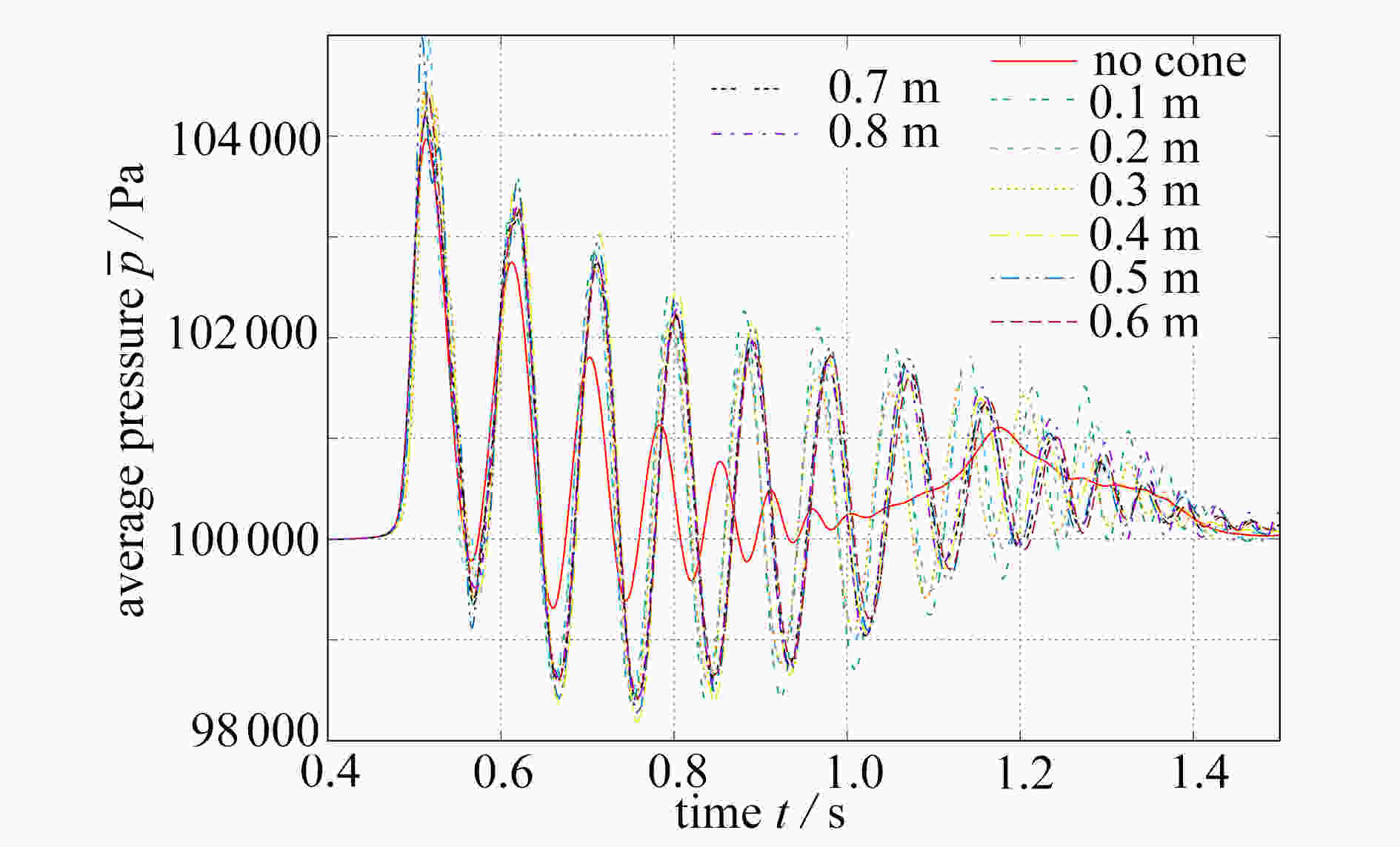
With the volume of fluid (VOF) method for a dam-break problem, the effects of wall structures on compressible bubble groups were studied through measurement of the spatial average pressure on the wall. An obstacle was set up at the bottom of the tank, which helps create air bubbles in the collapsing water impacting on it. Three kinds of structures were set up on the left wall, namely, a cuboidal structure, an ellipsoidal structure and a conical structure. It is found that when water hits the left wall, the topology of the bubble wrapped in the water will be changed by the wall structure, which leads to the change of pressure on the wall. The example analysis shows that, the cuboidal structure has the maximum effect in reducing the average pressure amplitude on the wall among those three kinds of wall structures. Especially, a proper adjustment of the position and the size of the cuboidal structure can eliminate the oscillation of the wall pressure.
Abstract:基于流体体积(VOF)法追踪自由液面，研究了壁面结构对三维可压缩气泡群流动的影响。通过在待测壁面上设置不同形状的壁面结构（长方体、椭球体和圆锥体）并改变它们各自的几何参数（位置和长度），来研究壁面结构对壁面附近的气泡群流动的影响，该影响表现为气泡群对壁面的空间平均压力。研究发现，壁面结构对气泡群的拓扑结构的影响会造成壁面压力的变化，其中长方体壁面结构降低壁面平均压力的效果最好，且通过适当调整该结构的位置和长度，能使壁面的压力脉动现象消失。
-
Key words:
- 可压缩两相流 /
- 气泡与壁面结构间耦合作用 /
- 流体体积法
-
Figure 1. Geometry and mesh of the computational domain with ellipsoids, cuboids and cones: (a) ellipsoidal wall structures; (b) cuboidal wall structures; (c) conical wall structures
Figure 2. Initial configuration of the static water column (ellipsoidal wall structures)
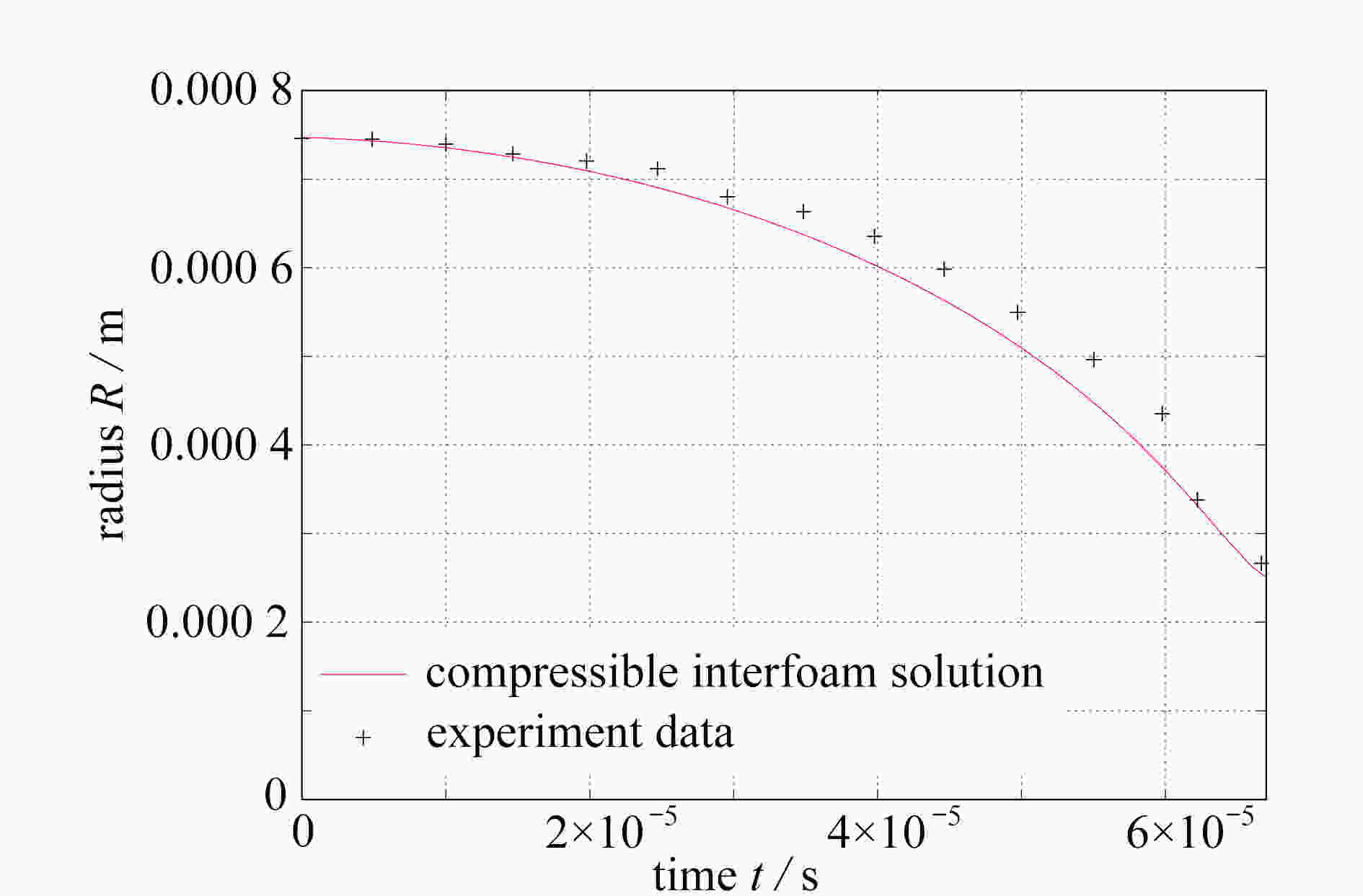
Figure 3. Comparison between the results of the codes used in this study and the experimental data[23]
Figure 4. Comparison of the results from cases where grid numbers are 65 536, 524 388 and 1 769 472, respectively: (a) 0~5 s; (b) 0.4~1.5 s
Figure 5. The impact process of wall structures, water and bubbles: (a) initial state; (b) before generation of bubbles; (c) generation of bubbles
Figure 7. Pressure and density distributions along the sample line at 0.5 s: (a) the sample line (white); (b) the pressure along the sample line; (c) the density along the sample line
Figure 8. Pressure and density distributions along the sample line at 0.57 s: (a) the sample line (white); (b) the pressure along the sample line;(c) the density along the sample line
Figure 9. Wall pressure evolutions: (a) the cases with ellipsoid height Lz = 0.2~0.8 m; (b) the case with Lz = 0.4 m and the no-ellipsoid case
Figure 10. Wall pressure evolutions and flow fields in the cases with ellipsoid height Lz = 0.1~0.3 m
Figure 11. Wall pressure evolutions and flow fields in the cases with ellipsoid height Lz = 0.5~0.7 m
Figure 13. The flow field in the ellipsoid wall structure case with ellipsoid height Ls = 0.4 m
Figure 18. The flow field in the cuboidal wall structure cases with cuboid heights Lz = 0.2 m and Ly = 0.5 m: (a) the flow profile; (b) the bubble contour
Table 1. Boundary conditions of each variable
wall boundary condition outlet boundary condition liquid phase fractional zero gradient inlet outlet pressure buoyant pressure total pressure velocity fixed value pressure inlet outlet velocity 
下载: 导出CSV
-
[1] CAPART H, YOUNG D L. Formation of a jump by the dam-break wave over a granular bed[J]. Journal of Fluid Mechanics, 1998, 372: 165-187. doi: 10.1017/S0022112098002250 [2] PRITCHARD D, HOGG A J. On sediment transport under dam-break flow[J]. Journal of Fluid Mechanics, 2002, 473: 265-274. doi: 10.1017/S0022112002002550 [3] LOBOVSKÝ L, BOTIA-VERA E, CASTELLANA F, et al. Experimental investigation of dynamic pressure loads during dam break[J]. Journal of Fluids & Structures, 2014, 48: 407-434. [4] MARTIN J C, MOYCE W J. Part Ⅳ: an experimental study of the collapse of liquid columns on a rigid horizontal plane philosophical[J]. Transactions of the Royal Society of London(Series A) : Mathematical and Physical Sciences, 1952, 244: 312-324. [5] KOSHIZUKA S, OKA Y. Moving-particle semi-implicit method for fragmentation of incompressible fluid[J]. Nuclear Science and Engineering, 1996, 123: 421-434. doi: 10.13182/NSE96-A24205 [6] CRUCHAGA M A, CELENTANO D J, TEZDUYAR T E. Collapse of a liquid column: numerical simulation and experimental validation[J]. Computational Mechanics, 2007, 39: 453-476. doi: 10.1007/s00466-006-0043-z [7] HU C, SUEYOSHI M. Numerical simulation and experiment on dam break problem[J]. Journal of Marine Science and Application, 2010, 9: 109-114. doi: 10.1007/s11804-010-9075-z [8] COLAGROSSI A, LANDRINI M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics[J]. Journal of Computational Physics, 2003, 191: 448-475. doi: 10.1016/S0021-9991(03)00324-3 [9] MA Z H, CAUSON D M, QIAN L, et al. A compressible multiphase flow model for violent aerated wave impact problems[J]. Proceedings of the Royal Society A: Mathematical Physical & Engineering Sciences, 2014, 470: 1-25. [10] SHIN S. Simulation of compressibility of entrapped air in an incompressible free surface flow using a pressure-based method for unified equations[J]. International Journal for Numerical Methods in Fluids, 2020, 92: 1274-1289. doi: 10.1002/fld.4827 [11] JANÍK P, HYHLÍK T. Pressure evaluation during dam break using weakly compressible SPH[J]. The European Physical Journal Conferences, 2019, 213: 02030. doi: 10.1051/epjconf/201921302030 [12] WANG L, JIANG Q, ZHANG C, et al. Improvements of MPS for reducing numerical pressure oscillation in the dam break simulation[J]. Advances in Water Science, 2018, 29(1): 89-99. [13] WANG X G, LUO C, GU Z B. Collapse simulation of a cavitation bubble near a rigid boundary[J]. Journal of Zhejiang University of Technology, 2015, 43(5): 512-516. [14] LI S, ZHANG A M, HAN R, et al. Experimental and numerical study on bubble-sphere interaction near a rigid wall[J]. Physics of Fluids, 2017, 29(9): 092102. doi: 10.1063/1.4993800 [15] BEIG S A, ABOULHASANZADEH B, JOHNSEN E. Temperatures produced by inertially collapsing bubbles near rigid surfaces[J]. Journal of Fluid Mechanics, 2018, 852: 102-125. [16] OpenCFD Ltd. OpenFOAM, the Open Source CFD Toolbox, User’s Guide[M]. Free Software Foundation, Inc, 2016. [17] NOH W F, WOODWARD P. SLIC (simple line interface calculation)[C]//Proceedings of the Fifth International Conference on Numerical Methods in Fluid Dynamics. Enschede: Twente University, 1976: 330-340. [18] WELLER H G. A new approach to VOF-based interface capturing methods for incompressible and compressible flow: TR/HGW/04[R]. Technical Report. OpenCFD Ltd, 2008. [19] FERZIGER J, PERIC M. Computational Methods for Fluid Dynamics[M]. Berlin: Springer, 2012. [20] ISSA R I. Solution of the implicitly discretised fluid flow equations by operator-splitting[J]. Journal of Computational Physics, 1986, 62(1): 40-65. doi: 10.1016/0021-9991(86)90099-9 [21] JASAK H, WELLER H G. Interface tracking capabilities of the inter-gamma differencing scheme[R]. London: Imperial College, University of London, 1995. [22] GUAN H, WANG J C, WEI Z J, et al. Numerical analysis of the interaction of 3D compressible bubble clusters[J]. Applied Mathematics and Mechanics (English Edition) , 2019, 40(8): 1181-1196. doi: 10.1007/s10483-019-2509-6 [23] KRÖNINGER D A. Particle-tracking-velocimetry-messungen an kollabierenden kavitationsblasen[D]. PhD Thesis. Göttingen: Georg-August Universität, 2008. -
计量
- 文章访问数: 572
- HTML全文浏览量: 201
- PDF下载量: 54
- 被引次数: 0
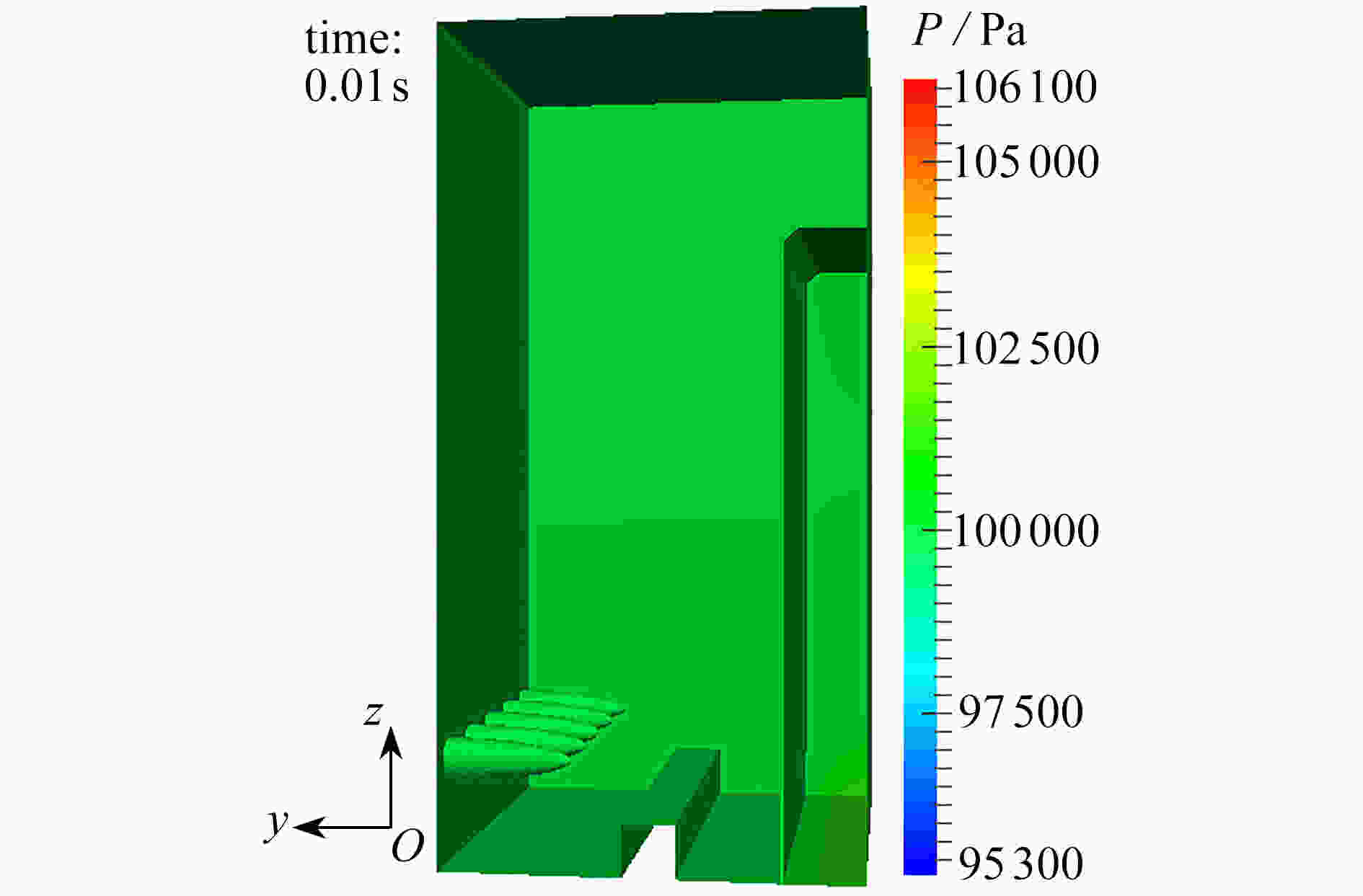
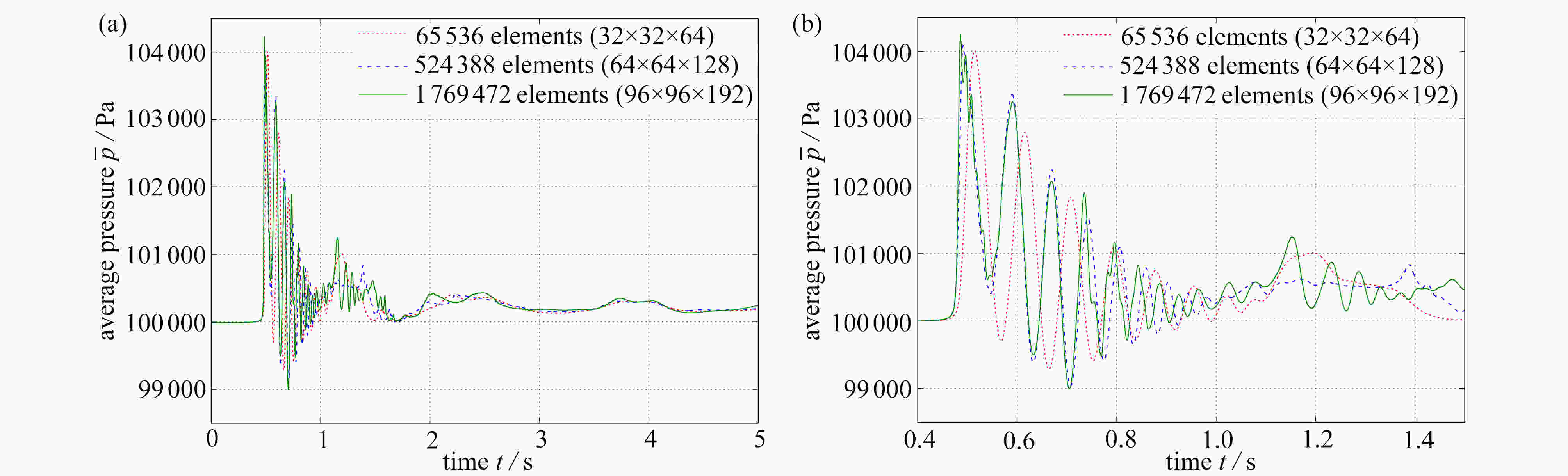
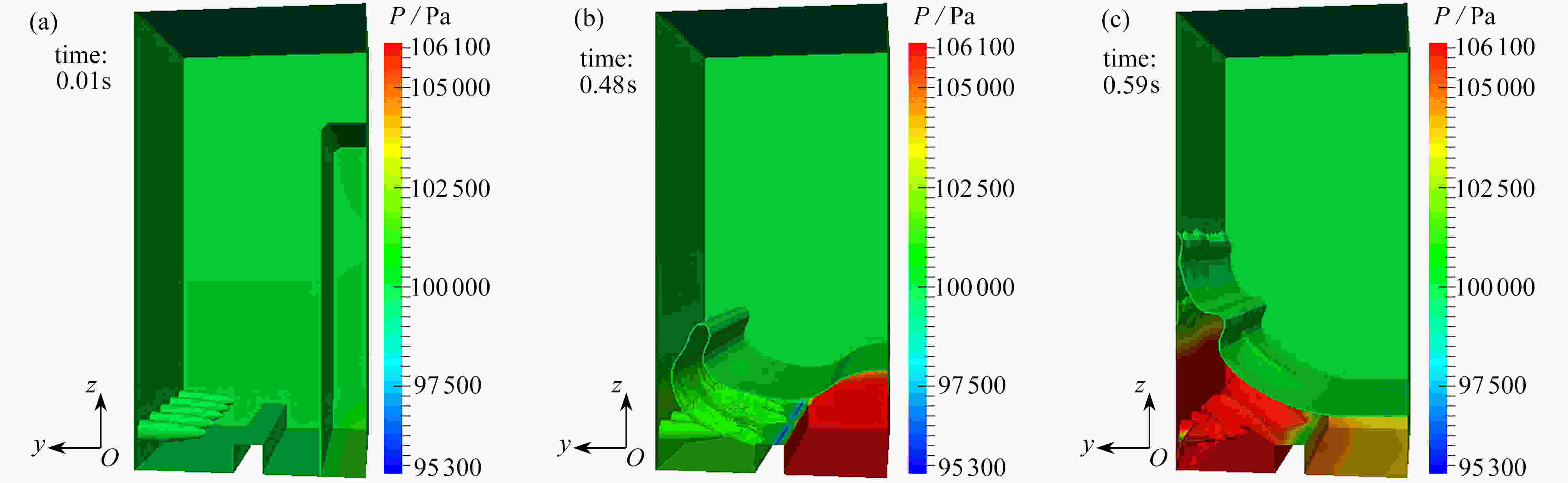
渝公网安备50010802005915号